Page 40 - Mathematical Techniques of Fractional Order Systems

30 Mathematical Techniques of Fractional Order Systems

Influence of θ
120
100
Bone mass z(t) [%] 80
60
40
20
0
0 200 400 600 800 1000 1200
1.05
Integer model
θ = 4e−08
1 θ = 6e−08
α(t) = 1 − θ T(t) 0.95 θ = 4e−07
θ = 8e−08
θ = 6e−07
0.9
θ = 8e−07
θ = 6e−06
0.85 θ = 4e−06
θ = 8e−06
0.8
0 200 400 600 800 1000 1200
Time t [days]
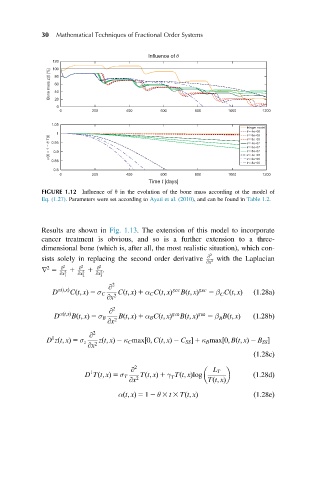
FIGURE 1.12 Influence of θ in the evolution of the bone mass according ot the model of
Eq. (1.27). Parameters were set according to Ayati et al. (2010), and can be found in Table 1.2.
Results are shown in Fig. 1.13. The extension of this model to incorporate
cancer treatment is obvious, and so is a further extension to a three-
dimensional bone (which is, after all, the most realistic situation), which con-
sists solely in replacing the second order derivative @ 2 2 with the Laplacian
@x
2
r 5 @ 2 2 1 @ 2 2 1 @ 2 2 .
@x @x @x
1 2 3
@ 2
D αðt;xÞ Cðt; xÞ 5 σ C Cðt; xÞ 1 α C Cðt; xÞ g CC Bðt; xÞ g BC 2 β Cðt; xÞ ð1:28aÞ
C
@x 2
@ 2
D αðt;xÞ Bðt; xÞ 5 σ B Bðt; xÞ 1 α B Cðt; xÞ g CB Bðt; xÞ g BB 2 β Bðt; xÞ ð1:28bÞ
B
@x 2
@ 2
1
½
½
D zðt; xÞ 5 σ z zðt; xÞ 2 κ C max 0; Cðt; xÞ 2 C SS Š 1 κ B max 0; Bðt; xÞ 2 B SS Š
@x 2
ð1:28cÞ
@ 2
1 L T
D Tðt; xÞ 5 σ T 2 Tðt; xÞ 1 γ Tðt; xÞlog ð1:28dÞ
T
@x Tðt; xÞ
αðt; xÞ 5 1 2 θ 3 t 3 Tðt; xÞ ð1:28eÞ