Page 41 - Mathematical Techniques of Fractional Order Systems

Variable Order Fractional Derivatives and Bone Remodeling Chapter | 1 31

5 4
4.5
Osteoclasts C(t) [cells] 3.5 3 2
2.5
1.5
0.5
0 1
0
0.1
0.2 2000
0.3
0.4 1400 1600 1800
0.5 1000 1200
0.6
0.7 800
0.8 600
0.9 200 400
Distance - x ∈ [0,1] 1 0 Time - t [days]
500
Osteoclasts B(t) [cells] 350
450
400
300
250
200
150
100
0
0
0.1
0.2
0.3 2000
0.4 1400 1600 1800
0.5 1000 1200
0.6
0.7 800
0.8 400 600
0.9 200
Distance - x ∈ [0,1] 1 0 Time - t [days]
2000
1800
Bone mass Z(t) [%] 100 90 80 70 60 50 800 1000 1200 1400
110
1600
40
0
0.1 400 600
0.2 0.3
0.4 Time - t [days]
0.5 200
0.6
0.7 0.8
0.9 1 0
Distance - x ∈ [0,1]
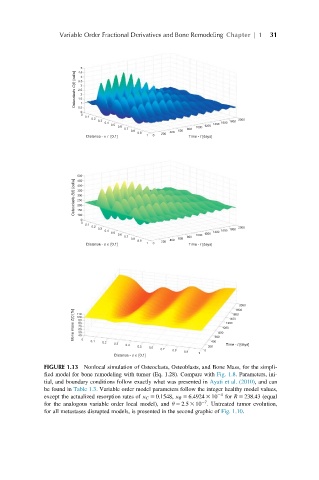
FIGURE 1.13 Nonlocal simulation of Osteoclasts, Osteoblasts, and Bone Mass, for the simpli-
fied model for bone remodeling with tumor (Eq. 1.28). Compare with Fig. 1.8. Parameters, ini-
tial, and boundary conditions follow exactly what was presented in Ayati et al. (2010), and can
be found in Table 1.3. Variable order model parameters follow the integer healthy model values,
except the actualized resorption rates of κ C 5 0:1548, κ B 5 6:4924 3 10 24 for R 5 238:43 (equal
27
for the analogous variable order local model), and θ 5 2:5 3 10 . Untreated tumor evolution,
for all metastases disrupted models, is presented in the second graphic of Fig. 1.10.