Page 35 - Mathematical Techniques of Fractional Order Systems

Variable Order Fractional Derivatives and Bone Remodeling Chapter | 1 25

8
7 6
Osteoclasts C(t) [cells] 5 4 3

1 2
0
0 0.1
0.2
0.3 4000
0.4 3000 3500
0.5 2500
0.6 2000
0.7 0.8 1000 1500
0.9 500
1 0
Distance - x ∈ [0,1] Time - t [days]
Osteoclasts B(t) [cells] 450
400
350
300
250
200
150
100
0
0.1
0.2
0.3
0.4 4000
0.5 3000 3500
0.6 2500
0.7 2000
0.8 1500
0.9 1000
Distance - x ∈ [0,1] 1 0 500
Time - t [days]
150
140
Bone mass Z(t) [%] 120 90
130
110
100
70 80 3500 4000
3000
60 2500
0
0.1 2000
0.2
0.3 1500
0.4 0.5
0.6 1000
0.7 500 Time - t [days]
0.8
0.9 1 0
Distance - x ∈ [0,1]
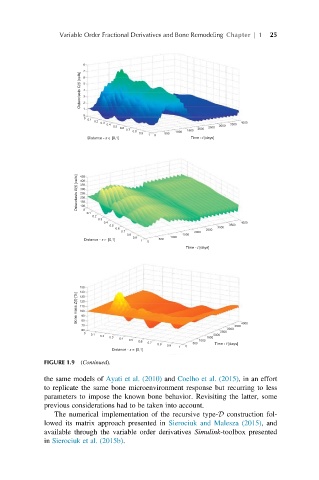
FIGURE 1.9 (Continued).
the same models of Ayati et al. (2010) and Coelho et al. (2015), in an effort
to replicate the same bone microenvironment response but recurring to less
parameters to impose the known bone behavior. Revisiting the latter, some
previous considerations had to be taken into account.
The numerical implementation of the recursive type-D construction fol-
lowed its matrix approach presented in Sierociuk and Malesza (2015), and
available through the variable order derivatives Simulink-toolbox presented
in Sierociuk et al. (2015b).