Page 425 - Mathematical Techniques of Fractional Order Systems
P. 425
410 Mathematical Techniques of Fractional Order Systems
α
D z 5 xy 2 bz; ð14:3Þ
where x is proportional to the intensity of the convective motion, y is propor-
tional to the temperature difference between the descending and ascending
currents and z is proportional to the distortion of the vertical temperature
profile from linearity (Lorenz, 1963). The system shows chaotic behavior at
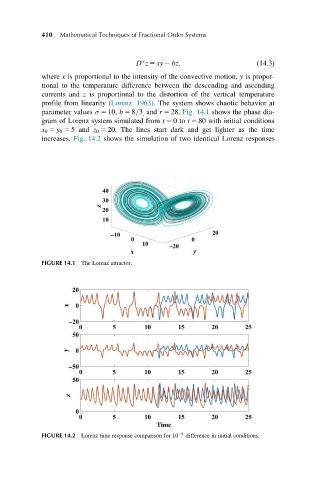
parameter values σ 5 10, b 5 8=3 , and r 5 28. Fig. 14.1 shows the phase dia-
gram of Lorenz system simulated from t 5 0to t 5 80 with initial conditions
x 0 5 y 0 5 5 and z 0 5 20. The lines start dark and get lighter as the time
increases. Fig. 14.2 shows the simulation of two identical Lorenz responses
FIGURE 14.1 The Lorenz attractor.
FIGURE 14.2 Lorenz time response comparison for 10 24 difference in initial conditions.