Page 434 - Mathematical Techniques of Fractional Order Systems

Applications of Continuous-time Fractional Order Chapter | 14 419

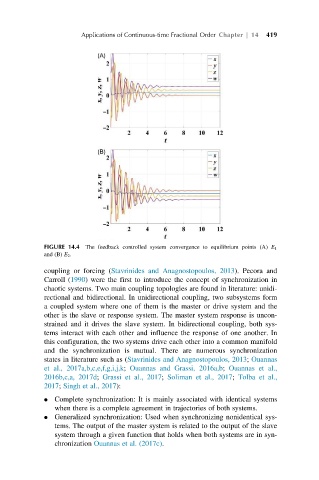
FIGURE 14.4 The feedback controlled system convergence to equilibrium points (A) E 1
and (B) E 2 .
coupling or forcing (Stavrinides and Anagnostopoulos, 2013). Pecora and
Carroll (1990) were the first to introduce the concept of synchronization in
chaotic systems. Two main coupling topologies are found in literature: unidi-
rectional and bidirectional. In unidirectional coupling, two subsystems form
a coupled system where one of them is the master or drive system and the
other is the slave or response system. The master system response is uncon-
strained and it drives the slave system. In bidirectional coupling, both sys-
tems interact with each other and influence the response of one another. In
this configuration, the two systems drive each other into a common manifold
and the synchronization is mutual. There are numerous synchronization
states in literature such as (Stavrinides and Anagnostopoulos, 2013; Ouannas
et al., 2017a,b,c,e,f,g,i,j,k; Ouannas and Grassi, 2016a,b; Ouannas et al.,
2016b,c,a, 2017d; Grassi et al., 2017; Soliman et al., 2017; Tolba et al.,
2017; Singh et al., 2017):
Complete synchronization: It is mainly associated with identical systems
when there is a complete agreement in trajectories of both systems.
Generalized synchronization: Used when synchronizing nonidentical sys-
tems. The output of the master system is related to the output of the slave
system through a given function that holds when both systems are in syn-
chronization Ouannas et al. (2017c).