Page 438 - Mathematical Techniques of Fractional Order Systems

Applications of Continuous-time Fractional Order Chapter | 14 423

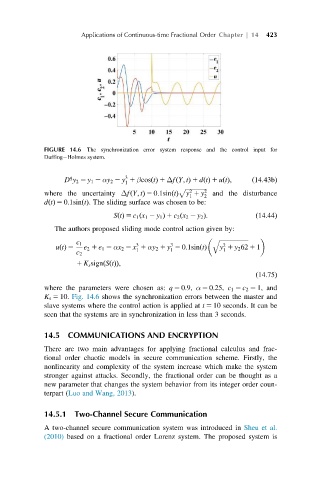
FIGURE 14.6 The synchronization error system response and the control input for
Duffing Holmes system.

3
q
D y 2 5 y 1 2 αy 2 2 y 1 βcosðtÞ 1 ΔfðY; tÞ 1 dðtÞ 1 uðtÞ; ð14:43bÞ
1
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
2
where the uncertainty ΔfðY; tÞ 5 0:1sinðtÞ y 1 y and the disturbance
1 2
dðtÞ 5 0:1sinðtÞ. The sliding surface was chosen to be:
SðtÞ 5 c 1 ðx 1 2 y 1 Þ 1 c 2 ðx 2 2 y 2 Þ: ð14:44Þ
The authors proposed sliding mode control action given by:

q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
c 1 3 3
uðtÞ 5 e 2 1 e 1 2 αx 2 2 x 1 αy 2 1 y 2 0:1sinðtÞ y 1 y 2 62 1 1
2
1
1
1
c 2
1 K s signðSðtÞÞ;
ð14:75Þ
where the parameters were chosen as: q 5 0:9, α 5 0:25, c 1 5 c 2 5 1, and
K s 5 10. Fig. 14.6 shows the synchronization errors between the master and
slave systems where the control action is applied at t 5 10 seconds. It can be
seen that the systems are in synchronization in less than 3 seconds.
14.5 COMMUNICATIONS AND ENCRYPTION
There are two main advantages for applying fractional calculus and frac-
tional order chaotic models in secure communication scheme. Firstly, the
nonlinearity and complexity of the system increase which make the system
stronger against attacks. Secondly, the fractional order can be thought as a
new parameter that changes the system behavior from its integer order coun-
terpart (Luo and Wang, 2013).

14.5.1 Two-Channel Secure Communication

A two-channel secure communication system was introduced in Sheu et al.
(2010) based on a fractional order Lorenz system. The proposed system is