Page 440 - Mathematical Techniques of Fractional Order Systems
P. 440
Applications of Continuous-time Fractional Order Chapter | 14 425
½x 1 ð0Þ; x 2 ð0Þ; x 3 ð0Þ 5 ½ 2 1; 2 2; 5; ð14:49cÞ
½y 1 ð0Þ; y 2 ð0Þ; y 3 ð0Þ 5 ½1; 2; 1: ð14:49dÞ
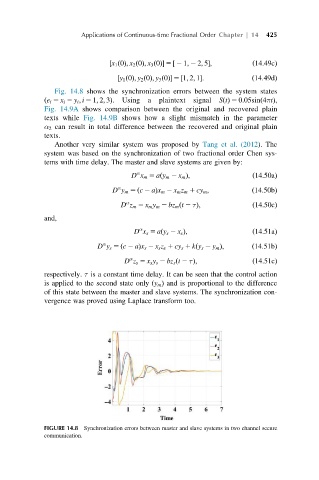
Fig. 14.8 shows the synchronization errors between the system states
ðe i 5 x i 2 y i ; i 5 1; 2; 3Þ. Using a plaintext signal SðtÞ 5 0:05sinð4πtÞ,
Fig. 14.9A shows comparison between the original and recovered plain
texts while Fig. 14.9B shows how a slight mismatch in the parameter
α 2 can result in total difference between the recovered and original plain
texts.
Another very similar system was proposed by Tang et al. (2012). The
system was based on the synchronization of two fractional order Chen sys-
tems with time delay. The master and slave systems are given by:
α
D x m 5 aðy m 2 x m Þ; ð14:50aÞ
α
D y m 5 ðc 2 aÞx m 2 x m z m 1 cy m ; ð14:50bÞ
α
D z m 5 x m y m 2 bz m ðt 2 τÞ; ð14:50cÞ
and,
α
D x s 5 aðy s 2 x s Þ; ð14:51aÞ
α
D y s 5 ðc 2 aÞx s 2 x s z s 1 cy s 1 kðy s 2 y m Þ; ð14:51bÞ
α
D z s 5 x s y s 2 bz s ðt 2 τÞ; ð14:51cÞ
respectively. τ is a constant time delay. It can be seen that the control action
is applied to the second state only ðy m Þ and is proportional to the difference
of this state between the master and slave systems. The synchronization con-
vergence was proved using Laplace transform too.
FIGURE 14.8 Synchronization errors between master and slave systems in two channel secure
communication.