Page 641 - Mathematical Techniques of Fractional Order Systems

612 Mathematical Techniques of Fractional Order Systems

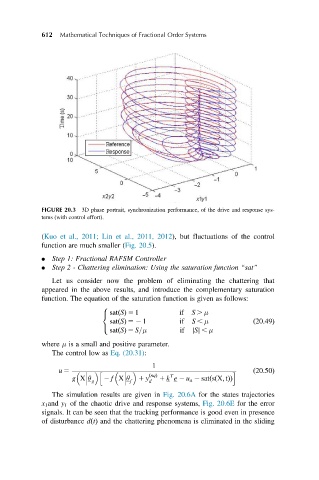
FIGURE 20.3 3D phase portrait, synchronization performance, of the drive and response sys-
tems (with control effort).

(Kuo et al., 2011; Lin et al., 2011, 2012), but fluctuations of the control
function are much smaller (Fig. 20.5).
Step 1: Fractional RAFSM Controller
Step 2 - Chattering elimination: Using the saturation function “sat”
Let us consider now the problem of eliminating the chattering that
appeared in the above results, and introduce the complementary saturation
function. The equation of the saturation function is given as follows:
8
satðSÞ 5 1 if S . μ
<
satðSÞ 52 1 if S , μ ð20:49Þ
satðSÞ 5 S=μ if S jj , μ
:
where μ is a small and positive parameter.
The control low as Eq. (20.31):
1
ð20:50Þ
u 5 h i
1 y 1 k e 2 u a 2 satðsðX; tÞÞ
ð nqÞ T
g X θ g 2 f X θ f d
The simulation results are given in Fig. 20.6A for the states trajectories
x 1 and y 1 of the chaotic drive and response systems, Fig. 20.6E for the error
signals. It can be seen that the tracking performance is good even in presence
of disturbance dðtÞ and the chattering phenomena is eliminated in the sliding