Page 30 - Mechanical Engineers' Handbook (Volume 2)

3 Statistics in the Measurement Process 19

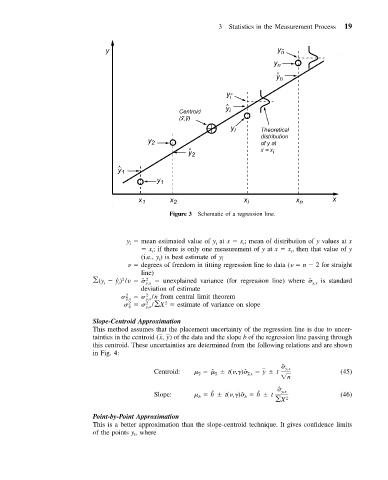
Figure 3 Schematic of a regression line.

y i mean estimated value of y at x x ; mean of distribution of y values at x
i
i
x ; if there is only one measurement of y at x x , then that value of y
i i
(i.e., y ) is best estimate of y
i i
degrees of freedom in fitting regression line to data ( n 2 for straight
line)
2
(y ) /v ˆ 2 unexplained variance (for regression line) where ˆ is standard
y
ˆ
i i y,x y,x
deviation of estimate
2 2 /n from central limit theorem
y,x y,x
2
2 b / X 2 estimate of variance on slope
y,x
Slope-Centroid Approximation
This method assumes that the placement uncertainty of the regression line is due to uncer-
tainties in the centroid (x, y ) of the data and the slope b of the regression line passing through
this centroid. These uncertainties are determined from the following relations and are shown
in Fig. 4:
ˆ y,x
Centroid: ˆ t( , )ˆ y,x y t (45)
y
y
n
ˆ y,x
ˆ
ˆ
Slope: b t( , )ˆ b t (46)
b
b
X 2
Point-by-Point Approximation
This is a better approximation than the slope-centroid technique. It gives confidence limits
y
of the points , where
i