Page 58 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

1.7 sprinG elements 55
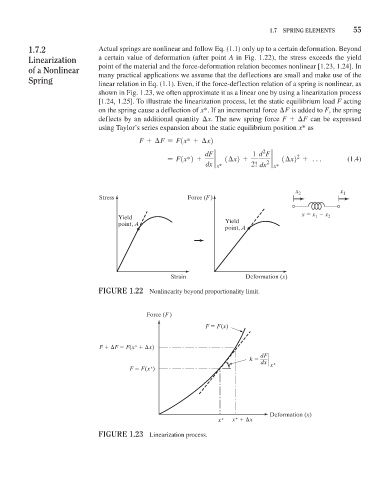
1.7.2 Actual springs are nonlinear and follow Eq. (1.1) only up to a certain deformation. Beyond
linearization a certain value of deformation (after point A in Fig. 1.22), the stress exceeds the yield
of a nonlinear point of the material and the force-deformation relation becomes nonlinear [1.23, 1.24]. In
many practical applications we assume that the deflections are small and make use of the
spring linear relation in Eq. (1.1). Even, if the force-deflection relation of a spring is nonlinear, as
shown in Fig. 1.23, we often approximate it as a linear one by using a linearization process
[1.24, 1.25]. To illustrate the linearization process, let the static equilibrium load F acting
on the spring cause a deflection of x*. If an incremental force F is added to F, the spring
deflects by an additional quantity x. The new spring force F + F can be expressed
using Taylor’s series expansion about the static equilibrium position x* as

F + F = F1x* + x2
2
dF 1 d F
2
= F1x*2 + 2 1 x2 + 2 1 x2 + c (1.4)
dx x* 2! dx 2 x*

x 2 x 1
Stress Force (F )

x x x
Yield 1 2
point, A Yield
point, A

Strain Deformation (x)
FiGure 1.22 Nonlinearity beyond proportionality limit.

Force (F )
F F(x)

F F F(x * x)
dF
k
dx x *
F F(x *)

Deformation (x)
x * x * x
FiGure 1.23 Linearization process.