Page 98 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

1.11 harmoniC analysis 95
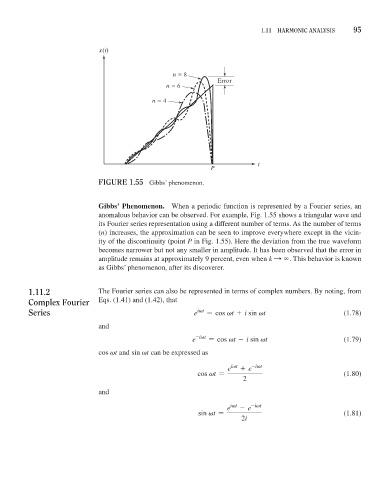
x(t)

n 8
Error
n 6

n 4

t
P
FiGure 1.55 Gibbs’ phenomenon.

Gibbs’ Phenomenon. When a periodic function is represented by a Fourier series, an
anomalous behavior can be observed. For example, Fig. 1.55 shows a triangular wave and
its Fourier series representation using a different number of terms. As the number of terms
(n) increases, the approximation can be seen to improve everywhere except in the vicin-
ity of the discontinuity (point P in Fig. 1.55). Here the deviation from the true waveform
becomes narrower but not any smaller in amplitude. It has been observed that the error in
amplitude remains at approximately 9 percent, even when k S . This behavior is known
as Gibbs’ phenomenon, after its discoverer.

1.11.2 The Fourier series can also be represented in terms of complex numbers. By noting, from
Complex Fourier Eqs. (1.41) and (1.42), that
series e ivt = cos vt + i sin vt (1.78)
and
e -ivt = cos vt - i sin vt (1.79)

cos vt and sin vt can be expressed as
e ivt + e -ivt
cos vt = (1.80)
2
and

e ivt - e -ivt
sin vt = (1.81)
2i