Page 95 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

92 Chapter 1 Fundamentals oF Vibration
Natural frequency. If a system, after an initial disturbance, is left to vibrate on its own,
the frequency with which it oscillates without external forces is known as its natural fre-
quency. As will be seen later, a vibratory system having n degrees of freedom will have, in
general, n distinct natural frequencies of vibration.

Beats. When two harmonic motions, with frequencies close to one another, are added, the
resulting motion exhibits a phenomenon known as beats. For example, if
x 1t2 = X cos vt (1.63)
1
x 1t2 = X cos1v + d2t (1.64)
2
where d is a small quantity, the addition of these motions yields
x1t2 = x 1t2 + x 1t2 = X [cos vt + cos1v + d2t] (1.65)
2
1
Using the relation
A + B A - B
cos A + cos B = 2 cos¢ ≤ cos¢ ≤ (1.66)
2 2
Eq. (1.65) can be rewritten as

dt d
x1t2 = 2X cos cos¢v + ≤ t (1.67)
2 2
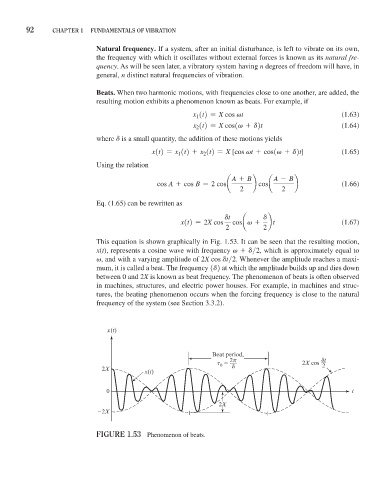
This equation is shown graphically in Fig. 1.53. It can be seen that the resulting motion,
x(t), represents a cosine wave with frequency v + d>2, which is approximately equal to
v, and with a varying amplitude of 2X cos dt>2. Whenever the amplitude reaches a maxi-
mum, it is called a beat. The frequency 1d2 at which the amplitude builds up and dies down
between 0 and 2X is known as beat frequency. The phenomenon of beats is often observed
in machines, structures, and electric power houses. For example, in machines and struc-
tures, the beating phenomenon occurs when the forcing frequency is close to the natural
frequency of the system (see Section 3.3.2).

x(t)

Beat period,
t 2p 2X cos dt
b
2
2X d
x(t)
0 t
2X
2X

FiGure 1.53 Phenomenon of beats.