Page 92 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

1.10 harmoniC motion 89
y

Im
X
A 2 sin u
X 2
X
v 1
A 2 cos u
a
u
vt
O x
A cos (vt a) Re
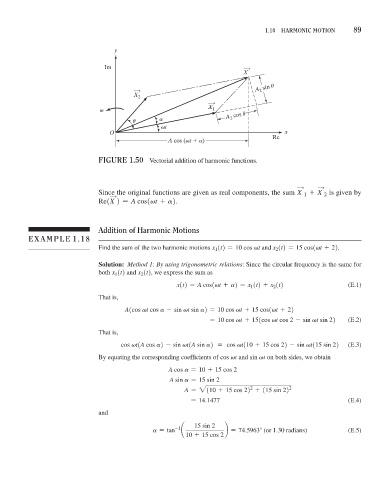
FiGure 1.50 Vectorial addition of harmonic functions.

> >
Since the original functions are given as real components, the sum X + X is given by
2
1
>
Re1X 2 = A cos1vt + a2.

addition of harmonic motions
example 1.18
Find the sum of the two harmonic motions x 1 1t2 = 10 cos vt and x 2 1t2 = 15 cos1vt + 22.

Solution: Method 1: By using trigonometric relations: Since the circular frequency is the same for
both x 1 1t2 and x 2 1t2, we express the sum as
x1t2 = A cos1vt + a2 = x 1 1t2 + x 2 1t2 (E.1)
That is,

A1cos vt cos a - sin vt sin a2 = 10 cos vt + 15 cos1vt + 22
= 10 cos vt + 151cos vt cos 2 - sin vt sin 22 (E.2)
That is,
cos vt1A cos a2 - sin vt1A sin a2 = cos vt110 + 15 cos 22 - sin vt115 sin 22 (E.3)

By equating the corresponding coefficients of cos vt and sin vt on both sides, we obtain
A cos a = 10 + 15 cos 2
A sin a = 15 sin 2
2 2
A = 2110 + 15 cos 22 + 115 sin 22
= 14.1477 (E.4)
and
15 sin 2
-1
a = tan ¢ ≤ = 74.5963 (or 1.30 radians) (E.5)
10 + 15 cos 2