Page 97 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

94 Chapter 1 Fundamentals oF Vibration
One-term approximation
Two-term approximation
x(t) x(t) Three-term approximation
Actual function
A A
A
2
0 0
t 2t 3t t t 2t 3t t
(a) (b)
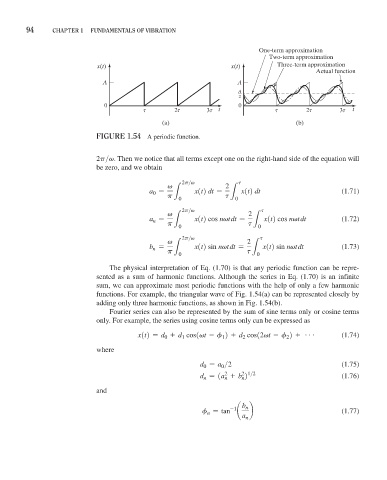
FiGure 1.54 A periodic function.

2p>v. Then we notice that all terms except one on the right-hand side of the equation will
be zero, and we obtain

2p>v t
v 2
a = x1t2 dt = x1t2 dt (1.71)
0
p L 0 t L 0
2p>v t
v 2
a = x1t2 cos nvt dt = x1t2 cos nvt dt (1.72)
n
p L 0 t L 0
2p>v t
v 2
b = x1t2 sin nvt dt = x1t2 sin nvt dt (1.73)
n
p L 0 t L 0
The physical interpretation of Eq. (1.70) is that any periodic function can be repre-
sented as a sum of harmonic functions. Although the series in Eq. (1.70) is an infinite
sum, we can approximate most periodic functions with the help of only a few harmonic
functions. For example, the triangular wave of Fig. 1.54(a) can be represented closely by
adding only three harmonic functions, as shown in Fig. 1.54(b).
Fourier series can also be represented by the sum of sine terms only or cosine terms
only. For example, the series using cosine terms only can be expressed as

x1t2 = d + d cos1vt - f 2 + d cos12vt - f 2 + g (1.74)
1
2
2
1
0
where
d = a >2 (1.75)
0
0
2 1>2
2
d = 1a + b 2 (1.76)
n
n
n
and
-1
f = tan ¢ a b n n ≤ (1.77)
n