Page 94 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

1.10 harmoniC motion 91
Period of oscillation. The time taken to complete one cycle of motion is known as the
period of oscillation or time period and is denoted by t. It is equal to the time required for
>
the vector OP in Fig. 1.47 to rotate through an angle of 2p and hence
2p
t = (1.59)
v
where v is called the circular frequency.

Frequency of oscillation. The number of cycles per unit time is called the frequency of
oscillation or simply the frequency and is denoted by f. Thus
1 v
f = = (1.60)
t 2p

Here v is called the circular frequency to distinguish it from the linear frequency
f = v>2p. The variable v denotes the angular velocity of the cyclic motion; f is measured
in cycles per second (hertz), while v is measured in radians per second.

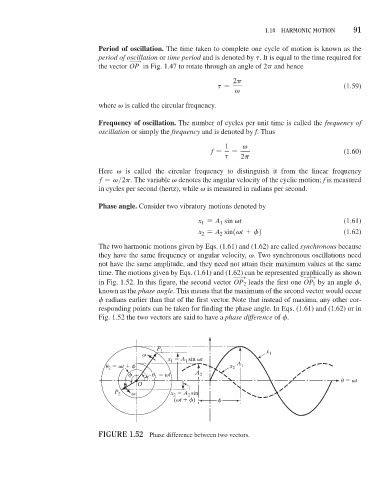
Phase angle. Consider two vibratory motions denoted by
x = A sin vt (1.61)
1
1
x = A sin1vt + f2 (1.62)
2
2
The two harmonic motions given by Eqs. (1.61) and (1.62) are called synchronous because
they have the same frequency or angular velocity, v. Two synchronous oscillations need
not have the same amplitude, and they need not attain their maximum values at the same
time. The motions given by Eqs. (1.61) and (1.62) can be represented graphically as shown
>
>
in Fig. 1.52. In this figure, the second vector OP leads the first one OP by an angle f,
1
2
known as the phase angle. This means that the maximum of the second vector would occur
f radians earlier than that of the first vector. Note that instead of maxima, any other cor-
responding points can be taken for finding the phase angle. In Eqs. (1.61) and (1.62) or in
Fig. 1.52 the two vectors are said to have a phase difference of f.

P 1 x
v 1
x A sin vt
1
1
u vt f x 2 A 1
2
f u vt A 2
1
O u vt
P 2 v x 2 A sin
2
(vt f) f

FiGure 1.52 Phase difference between two vectors.