Page 172 - Mechanics Analysis Composite Materials

Chapter 4. Mechanics of a composite layer 157

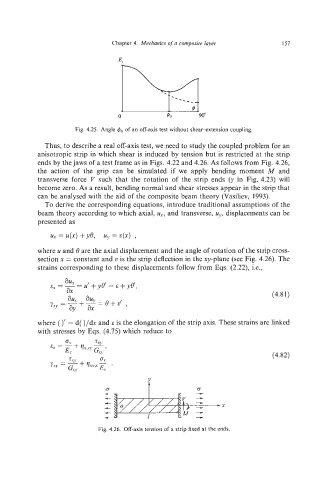
Fig. 4.25. Angle of an off-axis test without shear-extensioncoupling.

Thus, to describe a real off-axis test, we need to study the coupled problem for an
anisotropic strip in which shear is induced by tension but is restricted at the strip
ends by the jaws of a test frame as in Figs. 4.22 and 4.26. As follows from Fig. 4.26,
the action of the grip can be simulated if we apply bending moment M and
transverse force V such that the rotation of the strip ends (v in Fig. 4.23) will
become zero. As a result, bending normal and shear stresses appear in the strip that
can be analysed with the aid of the composite beam theory (Vasiliev, 1993).
To derive the corresponding equations, introduce traditional assumptions of the
beam theory according to which axial, u,, and transverse, up, displacements can be
presented as

u, = u(x) +yo, uJ.= u(x) ,
where u and 8 are the axial displacement and the angle of rotation of the strip cross-
section x = constant and u is the strip deflection in the xy-plane (see Fig. 4.26). The
strains corresponding to these displacements follow from Eqs. (2.22), Le.,

(4.81)
au,
au,,
y.r>, = -+-= 8 + u’ ,
ay ax
where ( )’ = d( )/dx and E is the elongation of the strip axis. These strains are linked
with stresses by Eqs. (4.75) which reduce to

(4.82)

f
0 d
f
+
f
f
f
c
Fig. 4.26. Off-axis tension of a strip fixed at the ends.