Page 176 - Mechanics Analysis Composite Materials

Chapter 4. Mechanics of a composite layer 161

where

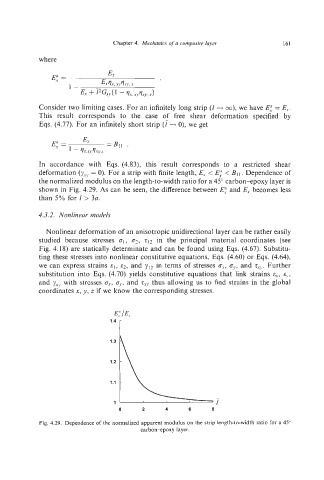
Consider two limiting cases. For an infinitely long strip (r+ m), we have E: = E,.
This result corresponds to the case of free shear deformation specified by
Eqs. (4.77). For an infinitely short strip (f+ 0), we get

In accordance with Eqs. (4.83), this result corresponds to a restricted shear
deformation (Y.~~,= 0). For a strip with finite length, E, < E.: < B1I. Dependence of
the normalized modulus on the length-to-width ratio for a 4.5" carbon+poxy layer is
shown in Fig. 4.29. As can be seen, the difference between and E,. becomes less
than 5% for I > 3a.

4.3.2. Non [inear models

Nonlinear deformation of an anisotropic unidirectional layer can be rather easily
studied because stresses 01, 02, ZIZ in the principal material coordinates (see
Fig. 4.18) are statically determinate and can be found using Eqs. (4.67). Substitu-
ting these stresses into nonlinear constitutive equations, Eqs. (4.60) or Eqs. (4.64),
we can express strains EI, EZ, and yI2 in terms of stresses a,, o,,,and zXy.Further
substitution into Eqs. (4.70) yields constitutive equations that. link strains c.~., c,.,
and y-vy with stresses a,, cy,and T~~ thus allowing us to find strains in the global
coordinates x,y, z if we know the corresponding stresses.

0 2 4 6 8

Fig. 4.29. Dependence of the normalized apparent modulus on the strip length-to-width ratio for a 45'
carbon-epoxy layer.