Page 292 - Mechanics Analysis Composite Materials

Chapter 6. Failure criteria and srrength of laminates 211

IT, ,MPa

IT,,MPa

-300
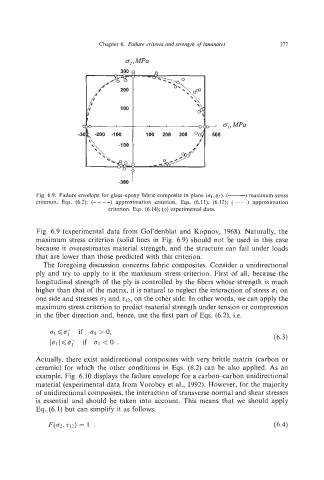
Fig. 6.9. Failure envelope for glass-epoxy fabric composite in plane (a1,CJ?).(-) maximum stress
criterion, Eqs. (6.2); (- -- -) approximation criterion, Eqs. (6.1I), (6.12); (. ....) approximation
criterion. Eqs. (6.14); (0) experimental data.

Fig. 6.9 (experimental data from Gol’denblat and Kopnov, 1968). Naturally, the
maximum stress criterion (solid lines in Fig. 6.9) should not be used in this case
because it overestimates material strength, and the structure can fail under loads
that are lower than those predicted with this criterion.
The foregoing discussion concerns fabric composites. Consider a unidirectional
ply and try to apply to it the maximum stress criterion. First of all, because the
longitudinal strength of the ply is controlled by the fibers whose strength is much
higher than that of the matrix, it is natural to neglect the interaction of stress GIon
one side and stresses 02 and TI?, on the other side. In other words, we can apply the
maximum stress criterion to predict material strength under tension or compression
in the fiber direction and, hence, use the first part of Eqs. (6.2), i.e.

Actually, there exist unidirectional composites with very brittle matrix (carbon or
ceramic) for which the other conditions in Eqs. (6.2) can be also applied. As an
example, Fig. 6.10 displays the failure envelope for a carbon-carbon unidirectional
material (experimental data from Vorobey et al., 1992). However, for the majority
of unidirectional composites, the interaction of transverse normal and shear stresses
is essential and should be taken into account. This means that we should apply
Eq. (6.1) but can simplify it as follows: