Page 345 - Mechanics Analysis Composite Materials

330 Mechanics and analysis of composite materials

where E =EI/(EI+E2).
To use Eqs. (7.42) for the inverse Laplace transformation, we should decompose
the right-hand part of Eq. (7.49) as

Applying Eqs. (7.42) we get

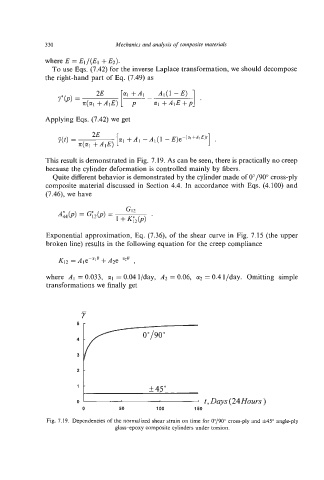
This result is demonstrated in Fig. 7.19. As can be seen, there is practically no creep
because the cylinder deformation is controlled mainly by fibers.
Quite different behavior is demonstrated by the cylinder made of 0"/90" cross-ply
composite material discussed in Section 4.4. In accordance with Eqs. (4.100) and
(7.46), we have

Exponential approximation, Eq. (7.36), of the shear curve in Fig. 7.15 (the upper
broken line) results in the following equation for the creep compliance

2
~ 1 =Ale-'IU +~2e-'t' ,
where AI = 0.033, 011 = 0.04 I/day, A2 = 0.06, u2 = 0.4 I/day. Omitting simple
transformations we finally get

r

:1

+45"

0 0 50 I00 150 t7Days(24Hours)
Fig. 7.19. Dependencies of the normalized shear strain on time for 0°/900cross-ply and *45" angle-ply
glass-epoxy composite cylinders under torsion.