Page 398 - Mechanics Analysis Composite Materials

Chapter 8. Oprimal composae structures 383
Integrating Eq. (8.53) under the condition 1/z‘ = 0 for r = R which means that
the tangent line to the shell meridian is parallel to axis z at r = R (see Fig. 8.4) we
arrive at

z‘ = - (8.55)

Further integration results in the following parametric equation for the shell
meridian:

Y
- = (I - t)”,
R

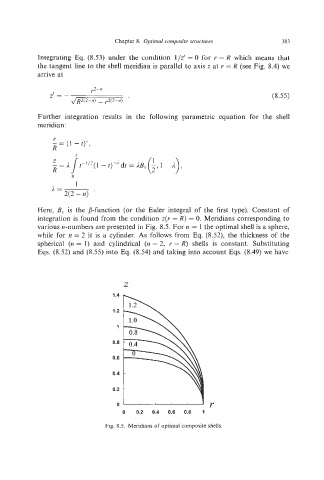
Here, B, is the a-function (or the Euler integral of the first type). Constant of
integration is found from the condition z(r =R) = 0. Meridians corresponding to
various n-numbers are presented in Fig. 8.5. For n = 1 the optimal shell is a sphere,
while for n = 2 it is a cylinder. As follows from Eq. (8.52), the thickness of the
spherical (n = 1) and cylindrical (n = 2, r = R) shells is constant. Substituting
Eqs. (8.52) and (8.55) into Eq. (8.54) and taking into account Eqs. (8.49) we have

1.4

1.2

1

0.8
0.6

0.4

0.2

0 I
0 0.2 0.4 0.6 0.8 1
Fig. 8.5. Meridians of optimal composite shells.