Page 401 - Mechanics Analysis Composite Materials

386 Mechanics and analysis of composite materials

Using this equation to transform Eq. (8.50) in which we take n = 0 and substituting
h from Eq. (8.57) we get the following equation for the longitudinal stress in the
tape:

p(R2 -4)+2roT
61 = (8.64)
2Rh~cos2&R
As can be seen, 01 does not depend on Y, and the optimal shell is a structure
reinforced with uniformly stressed fibers.
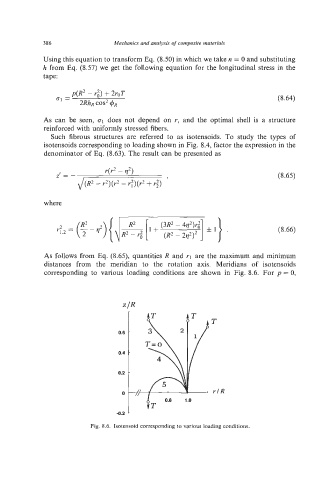
Such fibrous structures are referred to as isotensoids. To study the types of
isotensoids corresponding to loading shown in Fig. 8.4, factor the expression in the
denominator of Eq. (8.63). The result can be presented as

r(9 - q2)
z’ = - (8.65)
J(R2 - r2)(r2- rf)(r2+r;2) ’

where

6.2 = (8.66)

As follows from Eq. (8.65), quantities R and r-1 are the maximum and minimum
distances from the meridian to the rotation axis. Meridians of isotensoids
corresponding to various loading conditions are shown in Fig. 8.6. For p = 0,

i’

0.6

0.4

0.2

rlR
0 I
0.8 1.0
QT
-0.2
Fig. 8.6. Isotensoid corresponding to various loading conditions.