Page 321 - Mechanics of Asphalt Microstructure and Micromechanics
P. 321
Applications of Discrete Element Method 313
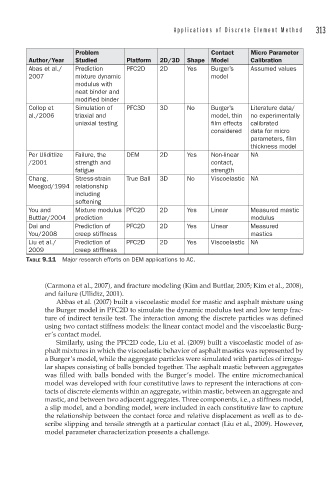
Problem Contact Micro Parameter
Author/Year Studied Platform 2D/3D Shape Model Calibration
Abas et al./ Prediction PFC2D 2D Yes Burger’s Assumed values
2007 mixture dynamic model
modulus with
neat binder and
modified binder
Collop et Simulation of PFC3D 3D No Burger’s Literature data/
al./2006 triaxial and model, thin no experimentally
uniaxial testing film effects calibrated
considered data for micro
parameters, film
thickness model
Per Uliditlize Failure, the DEM 2D Yes Non-linear NA
/2001 strength and contact,
fatigue strength
Chang, Stress-strain True Ball 3D No Viscoelastic NA
Meegod/1994 relationship
including
softening
You and Mixture modulus PFC2D 2D Yes Linear Measured mastic
Buttlar/2004 prediction modulus
Dai and Prediction of PFC2D 2D Yes Linear Measured
You/2008 creep stiffness mastics
Liu et al./ Prediction of PFC2D 2D Yes Viscoelastic NA
2009 creep stiffness
TABLE 9.11 Major research efforts on DEM applications to AC.
(Carmona et al., 2007), and fracture modeling (Kim and Buttlar, 2005; Kim et al., 2008),
and failure (Ullidtz, 2001).
Abbas et al. (2007) built a viscoelastic model for mastic and asphalt mixture using
the Burger model in PFC2D to simulate the dynamic modulus test and low temp frac-
ture of indirect tensile test. The interaction among the discrete particles was defined
using two contact stiffness models: the linear contact model and the viscoelastic Burg-
er’s contact model.
Similarly, using the PFC2D code, Liu et al. (2009) built a viscoelastic model of as-
phalt mixtures in which the viscoelastic behavior of asphalt mastics was represented by
a Burger’s model, while the aggregate particles were simulated with particles of irregu-
lar shapes consisting of balls bonded together. The asphalt mastic between aggregates
was filled with balls bonded with the Burger’s model. The entire micromechanical
model was developed with four constitutive laws to represent the interactions at con-
tacts of discrete elements within an aggregate, within mastic, between an aggregate and
mastic, and between two adjacent aggregates. Three components, i.e., a stiffness model,
a slip model, and a bonding model, were included in each constitutive law to capture
the relationship between the contact force and relative displacement as well as to de-
scribe slipping and tensile strength at a particular contact (Liu et al., 2009). However,
model parameter characterization presents a challenge.