Page 316 - Mechanics of Asphalt Microstructure and Micromechanics

308 Ch a p t e r N i n e

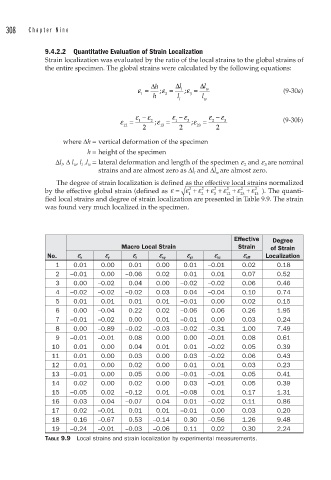
9.4.2.2 Quantitative Evaluation of Strain Localization
Strain localization was evaluated by the ratio of the local strains to the global strains of
the entire specimen. The global strains were calculated by the following equations:

Δh Δl Δl
ε = ; ε = l ; ε = w (9-30a)
1 h 2 l 3 l
l w
ε − ε ε − ε ε − ε
ε = 1 2 ; ε = 1 3 ; ε = 2 3 (9-30b)
12 2 13 2 23 2
where Δh = vertical deformation of the specimen
h = height of the specimen
Δl l , Δ l w , l l ,l w = lateral deformation and length of the specimen e 2 and e 3 are nominal
strains and are almost zero as Δl l and Δl w are almost zero.
The degree of strain localization is defined as the effective local strains normalized
by the effective global strain (defined as ε = ε + ε + ε + ε + ε + ε 2 ). The quanti-
2
2
2
2
2
1 2 3 12 23 13
fied local strains and degree of strain localization are presented in Table 9.9. The strain
was found very much localized in the specimen.
Effective Degree
Macro Local Strain Strain of Strain
No. d x d y d z d xy d yz d xz d eff Localization
1 0.01 0.00 0.01 0.00 0.01 –0.01 0.02 0.18
2 –0.01 0.00 –0.06 0.02 0.01 0.01 0.07 0.52
3 0.00 –0.02 0.04 0.00 –0.02 –0.02 0.06 0.46
4 –0.02 –0.02 –0.02 0.03 0.04 –0.04 0.10 0.74
5 0.01 0.01 0.01 0.01 –0.01 0.00 0.02 0.15
6 0.00 –0.04 0.22 0.02 –0.06 0.06 0.26 1.95
7 –0.01 –0.02 0.00 0.01 –0.01 0.00 0.03 0.24
8 0.00 –0.89 –0.02 –0.03 –0.02 –0.31 1.00 7.49
9 –0.01 –0.01 0.08 0.00 0.00 –0.01 0.08 0.61
10 0.01 0.00 0.04 0.01 0.01 –0.02 0.05 0.39
11 0.01 0.00 0.03 0.00 0.03 –0.02 0.06 0.43
12 0.01 0.00 0.02 0.00 0.01 0.01 0.03 0.23
13 –0.01 0.00 0.05 0.00 –0.01 –0.01 0.05 0.41
14 0.02 0.00 0.02 0.00 0.03 –0.01 0.05 0.39
15 –0.05 0.02 –0.12 0.01 –0.08 0.01 0.17 1.31
16 0.03 0.04 –0.07 0.04 0.01 –0.02 0.11 0.86
17 0.02 –0.01 0.01 0.01 –0.01 0.00 0.03 0.20
18 0.16 –0.67 0.53 –0.14 0.30 –0.56 1.26 9.48
19 –0.24 –0.01 –0.03 –0.06 0.11 0.02 0.30 2.24
TABLE 9.9 Local strains and strain localization by experimental measurements.