Page 67 - Mechanics of Asphalt Microstructure and Micromechanics

60 Ch a p t e r Th r e e

diagnosis. X-ray radiography is basically a two-dimensional (2D) picture (overall pro-
jection of the attenuation properties on one plane). Due to the projection, the three-di-
mensional (3D) details of the materials were smeared. XCT is a revolutionary improve-
ment over X-ray radiography. It was invented more than a half century after the dis-
covery of X-ray. This invention initiated a revolution in medical diagnosis; both inven-
tors, Allan M. Cormack and Godfrey N. Hounsfield, were awarded the Nobel Prize in
1979. The following section illustrates the fundamentals of XCT.
X-rays have very high penetrating capability and can penetrate into solids such as
metals, stones, and asphalt mixtures. When X-rays penetrate into a material, its inten-
sity (energy per unit area per unit time) becomes attenuated due to the absorption and
scattering of X-rays by the atoms of the material. Different materials attenuate X-rays at
different rates. Therefore, by penetrating X-rays into different materials and measuring
their attenuations (the difference between the intensity before penetration and the in-
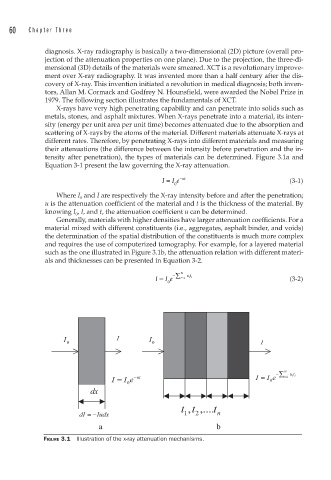
tensity after penetration), the types of materials can be determined. Figure 3.1a and
Equation 3-1 present the law governing the X-ray attenuation.
I = I e − ut (3-1)
0
Where I 0 and I are respectively the X-ray intensity before and after the penetration;
u is the attenuation coefficient of the material and t is the thickness of the material. By
knowing I 0 , I, and t, the attenuation coefficient u can be determined.
Generally, materials with higher densities have larger attenuation coefficients. For a
material mixed with different constituents (i.e., aggregates, asphalt binder, and voids)
the determination of the spatial distribution of the constituents is much more complex
and requires the use of computerized tomography. For example, for a layered material
such as the one illustrated in Figure 3.1b, the attenuation relation with different materi-
als and thicknesses can be presented in Equation 3-2.

I = I e − N i ∑ =1 ut ii (3-2)
0

FIGURE 3.1 Illustration of the x-ray attenuation mechanisms.