Page 279 - Mechanics of Microelectromechanical Systems

266 Chapter 5

The values of and define the point P of Fig. 5.2, which characterizes the
phenomenon known as pull-in. For forces less than of Eq. (5.8), the slope
of the electrostatic force is smaller than the one of the spring force (which is
equivalent to saying that the slope of the total force F is less than zero) and
the system is stable. When the forces are larger than the situation reverses
and the slope of F is greater than zero, which means that the system becomes
unstable. As a consequence, for displacements that are larger than one-third
of the initial gap the mobile plate collapses (it is pulled-in) against the
fixed one, irrespective of the microspring design. This also explains the
reason why the equilibrium point is stable (it is positioned to the left of
and the other equilibrium point is unstable.
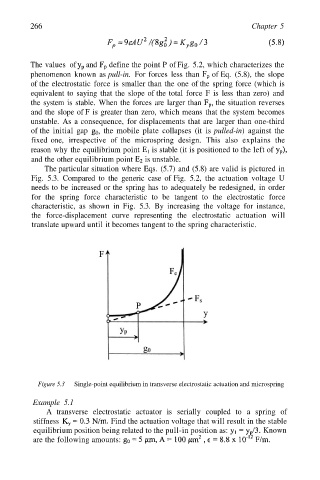
The particular situation where Eqs. (5.7) and (5.8) are valid is pictured in
Fig. 5.3. Compared to the generic case of Fig. 5.2, the actuation voltage U
needs to be increased or the spring has to adequately be redesigned, in order
for the spring force characteristic to be tangent to the electrostatic force
characteristic, as shown in Fig. 5.3. By increasing the voltage for instance,
the force-displacement curve representing the electrostatic actuation will
translate upward until it becomes tangent to the spring characteristic.

Figure 5.3 Single-point equilibrium in transverse electrostatic actuation and microspring

Example 5.1
A transverse electrostatic actuator is serially coupled to a spring of
stiffness Find the actuation voltage that will result in the stable
equilibrium position being related to the pull-in position as: Known
are the following amounts: