Page 107 - Mechanism and Theory in Organic Chemistry

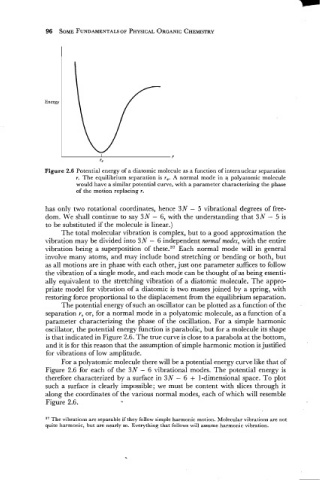
Figure 2.6 Potential energy of a diatomic molecule as a function of internuclear separation
r. The equilibrium separation is re. A normal mode in a polyatomic molecule
would have a similar potential curve, with a parameter characterizing the phase
of the motion replacing r.

has only two rotational coordinates, hence 3N - 5 vibrational degrees of free-
dom. We shall continue to say 3 N - 6, with the understanding that 3 N - 5 is
to be substituted if the molecule is linear.)
The total molecular vibration is complex, but to a good approximation the
vibration may be divided into 3N - 6 independent normal modes, with the entire
vibration being a superposition of these.37 Each normal mode will in general
involve many atoms, and may include bond stretching or bending or both, but
as all motions are in phase with each other, just one parameter suffices to follow
the vibration of a single mode, and each mode can be thought of as being essenti-
ally equivalent to the stretching vibration of a diatomic molecule. The appro-
priate model for vibration of a diatomic is two masses joined by a spring, with
restoring force proportional to the displacement from the equilibrium separation.
The potential energy of such an oscillator can be plotted as a function of the
separation r, or, for a normal mode in a polyatomic molecule, as a function of a
parameter characterizing the phase of the oscillation. For a simple harmonic
oscillator, the potential energy function is parabolic, but for a molecule its shape
is that indicated in Figure 2.6. The true curve is close to a parabola at the bottom,
and it is for this reason that the assumption of simple harmonic motion is justified
for vibrations of low amplitude.
For a polyatomic molecule there will be a potential energy curve like that of
Figure 2.6 for each of the 3N - 6 vibrational modes. The potential energy is
therefore characterized by a surface in 3N - 6 + 1-dimensional space. To plot
such a surface is clearly impossible; we must be content with slices through it
along the coordinates of the various normal modes, each of which will resemble
Figure 2.6.

37 The vibrations are separable if they follow simple harmonic motion. Molecular vibrations are not
quite harmonic, but are nearly so. Everything that follows will assume harmonic vibration.