Page 100 -

90 3 Optical Tweezers
∞
n cos α − R cos(α − β)
R cos(α + nβ)= ,
1 − 2R cos β + R 2
n=0
∞
n sin α − R sin(α − β)
R sin(α + nβ)= .
1 − 2R cos β + R 2
n=0
Since θ 2 =arcsin{(n 1 /n 2 )sin θ 1 },R is from (3.2), and T is from (3.3), we can
express (3.5) and (3.6) usinga ray incident angle θ 1 .
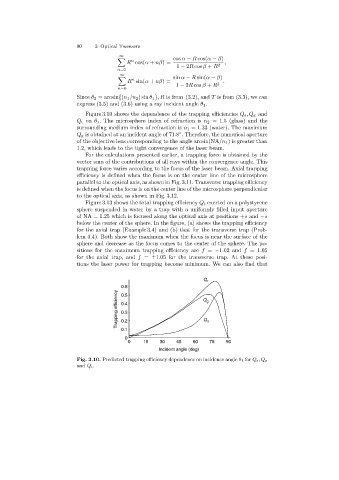
Figure 3.10 shows the dependence of the trapping efficiencies Q s ,Q g and
Q t on θ 1 . The microsphere index of refraction is n 2 =1.5 (glass) and the
surroundingmedium index of refraction is n 1 =1.33 (water). The maximum
Q g is obtained at an incident angle of 71.8 . Therefore, the numerical aperture
◦
of the objective lens correspondingto the angle arcsin(NA/n 1 ) is greater than
1.2, which leads to the tight convergence of the laser beam.
For the calculations presented earlier, a trappingforce is obtained by the
vector sum of the contributions of all rays within the convergence angle. This
trappingforce varies accordingto the focus of the laser beam. Axial trapping
efficiency is defined when the focus is on the center line of the microsphere
parallel to the optical axis, as shown in Fig. 3.11. Transverse trapping efficiency
is defined when the focus is on the center line of the microsphere perpendicular
to the optical axis, as shown in Fig. 3.12.
Figure 3.13 shows the total trapping efficiency Q t exerted on a polystyrene
sphere suspended in water by a trap with a uniformly filled input aperture
of NA = 1.25 which is focused alongthe optical axis at positions +s and −s
below the center of the sphere. In the figure, (a) shows the trapping efficiency
for the axial trap (Example 3.4) and (b) that for the transverse trap (Prob-
lem 3.4). Both show the maximum when the focus is near the surface of the
sphere and decrease as the focus comes to the center of the sphere. The po-
sitions for the maximum trappingefficiency are f = −1.02 and f =1.05
for the axial trap, and f = ±1.05 for the transverse trap. At these posi-
tions the laser power for trappingbecome minimum. We can also find that

Q t
0.6
Trapping efficiency 0.4 Q g
0.5

0.3
Q
0.2
0.1 s
0
0 15 30 45 60 75 90
Incident angle (deg)

Fig. 3.10. Predicted trapping efficiency dependence on incidence angle θ 1 for Q s,Q g
and Q t.