Page 259 - Microtectonics

9.3 · Vorticity Gauges 251
ratio and quartz LPO pattern asymmetry, and Ratsch-
bacher et al. (1991) used the orientation of the c-axis
maxima of calcite LPO patterns.
In flow with a monoclinic symmetry, the central axis
of a quartz-c-axis pattern in a stereogram should be ap-
proximately at right angles to the flow plane of the de-
formation responsible for the fabric development. The
orientation of a foliation formed in a single deformation
event with respect to this flow plane is a function of W
k
and finite strain. Therefore, if quartz fabric patterns are
used to determine the orientation of the flow plane in a
foliated rock, the angle between the foliation and this flow
plane can be used to find W provided that finite strain
m
can be determined independently (Wallis 1992a, 1995;
Graseman et al. 1999; Law et al. 2004; Fig. 9.1).

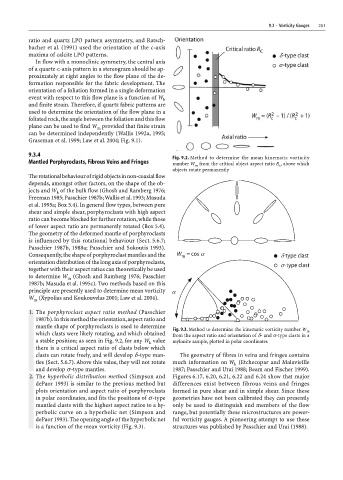
9.3.4 Fig. 9.2. Method to determine the mean kinematic vorticity
Mantled Porphyroclasts, Fibrous Veins and Fringes number W m from the critical object aspect ratio R c , above which
objects rotate permanently
The rotational behaviour of rigid objects in non-coaxial flow
depends, amongst other factors, on the shape of the ob-
jects and W of the bulk flow (Ghosh and Ramberg 1976;
k
Freeman 1985; Passchier 1987b; Wallis et al. 1993; Masuda
et al. 1995a; Box 5.4). In general flow types, between pure
shear and simple shear, porphyroclasts with high aspect
ratio can become blocked for further rotation, while those
of lower aspect ratio are permanently rotated (Box 5.4).
The geometry of the deformed mantle of porphyroclasts
is influenced by this rotational behaviour (Sect. 5.6.7;
Passchier 1987b, 1988a; Passchier and Sokoutis 1993).
Consequently, the shape of porphyroclast mantles and the
orientation distribution of the long axis of porphyroclasts,
together with their aspect ratios can theoretically be used
to determine W (Ghosh and Ramberg 1976; Passchier
m
1987b; Masuda et al. 1995c). Two methods based on this
principle are presently used to determine mean vorticity
W (Xypolias and Koukouvelas 2001; Law et al. 2004).
m
1. The porphyroclast aspect ratio method (Passchier
1987b). In this method the orientation, aspect ratio and
mantle shape of porphyroclasts is used to determine
Fig. 9.3. Method to determine the kinematic vorticity number W m
which clasts were likely rotating, and which obtained from the aspect ratio and orientation of δ- and σ-type clasts in a
a stable position; as seen in Fig. 9.2, for any W value mylonite sample, plotted in polar coordinates
k
there is a critical aspect ratio of clasts below which
clasts can rotate freely, and will develop δ-type man- The geometry of fibres in veins and fringes contains
tles (Sect. 5.6.7). Above this value, they will not rotate much information on W (Etchecopar and Malavieille
k
and develop σ-type mantles. 1987; Passchier and Urai 1988; Beam and Fischer 1999).
2. The hyperbolic distribution method (Simpson and Figures 6.17, 6.20, 6.21, 6.22 and 6.24 show that major
dePaor 1993) is similar to the previous method but differences exist between fibrous veins and fringes
plots orientation and aspect ratio of porphyroclasts formed in pure shear and in simple shear. Since these
in polar coordinates, and fits the positions of σ-type geometries have not been calibrated they can presently
mantled clasts with the highest aspect ratios to a hy- only be used to distinguish end members of the flow
perbolic curve on a hyperbolic net (Simpson and range, but potentially these microstructures are power-
dePaor 1993). The opening angle of the hyperbolic net ful vorticity gauges. A pioneering attempt to use these
is a function of the mean vorticity (Fig. 9.3). structures was published by Passchier and Urai (1988).