Page 513 - Modelling in Transport Phenomena A Conceptual Approach

A.2. MEAN VALUE TmOREM 493

A.2 MEAN VALUE THEORJ3M

If f(z) is continuous in the interval a 5 x 5 b, then the value of the integration of
f(z) over an interval z = a to z = b is
b
I = lb f(x) dx = (f) / dz = (f)(b - a) (A.2-1)
a
where (f) is the average value of f in the interval a 5 z 5 b.
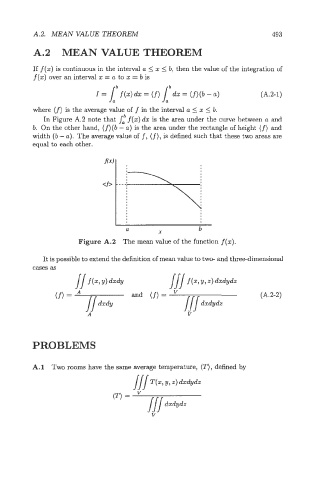
In Figure A.2 note that s,” f(z) dx is the area under the curve between a and
b. On the other hand, (f)(b - a) is the area under the rectangle of height (f) and
width (b - a). The average value of f, (f), is defined such that these two areas are
equal to each other.

~~
a X b
Figure A.2 The mean value of the function f(x).

It is possible to extend the definition of mean value to two- and three-dimensional
cases as

JJ f (2, Y) dXdY JJJ f(x, Y, .4 dxdydz
A (A.2-2)
(f) = and (f) = V
JJJ dxdydz
/bdY V
A

PROBLEMS

A.l Two rooms have the same average temperature, (T), defined by