Page 130 - Modern Spatiotemporal Geostatistics

1
1
1
1
1
1
1
1
th
th
th
o
o
o
e
BM
BM
the
e
e
o
Formulation
Formulatio
Formulatio
Mathematica
Mathematical
Mathematica
n
n
n
Formulatio
Mathematica
Mathematica l l l l Formulatio n of f f f f th e BME Method 1111 1 1 1
BM
Metho
Metho
Metho
Metho
d
d
d
d
BM
E
E
E
E
physica
physica
o
o
o
physical laws..
BM
5.1
BM
physica
BM
E
E
E
e
e
analysi
analysi
BME
e
analysis off
analysi
Figure
5.1.
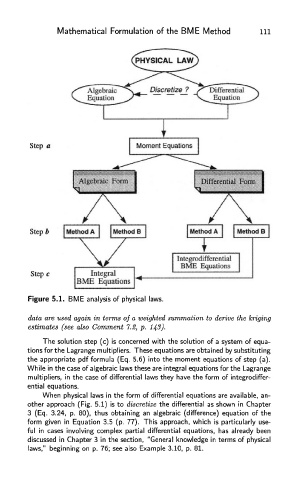
Figur e 5.1 . . . . BM E analysi s s s s o f f f physica l l l l laws . . .
laws
laws
5.1
Figur
laws
Figur
5.1
Figur
to
summation
are
kriging
in
are
kriging
kriging
are
again
data
again
data are used again in terms of a weighted summation to derive the kriging
again
summation
summation
data
data
data are used again in terms of a weighted summation to derive the kriging
in
used
a
a
of
of
of
weighted
used
used
a
weighted
weighted
the
terms
terms
terms
the
the
derive
derive
derive
in
to
to
(see
(see
(see
p.
p.
7.2,
p.
14$)-
14$)-
14$)-
7.2,
also
also
also
Comment
7.2,
Comment
Comment
estimates
estimates (see also Comment 7.2, p. 143)-
estimates
estimates
estimates (see also Comment 7.2, p. 14$)-
Th
Th
h
Th
th
th
thee
th
m
wit
wit
m
m
m
wit
Th
h
h
p
p
Thee solutio n ste p (c ) ) ) i i i is concerned withh th e solutio n off f f f a system of equa-- - - -
o
o
o
a
a
o
solutio
n
n
n
solutio
solutio
n
syste
e
e
syste
syste
syste
ste
solutionn
a
a
stepp
ste
ste
o
(c))
equa
equa
(c
(c
(c
f
f
f
equa
equa
f
s
s
e
e
e
i
concerne
concerne
concerne
s
s
concerne
solutio
wit
d
d
o
o
o
d
solutio
solutio
solutionn
d
s
fo
multipliers
e
multipliers
e
ar
e
e
ar
s
s
ar
e
e
Thes
Thes
Thes
These equations are obtainedd
e
e
fo
equation
equation
multipliers
equation
s
fo
s
s
e
tions for thee
b
th
substitutin
substitutin
d
d
b
by substitutingg
b
Lagrang
tion
substitutin
e
tion
e
th
th
Lagrang
Lagrang
Lagrange multipliers..
g
obtaine
obtaine
g
tion s fo r r r r th e Lagrang e multipliers . . . Thes e equation s ar e obtaine d b y y y y substitutin g
tion
obtaine
stepp
into thee
pdf formulaa
int
int
int
(Eq
(Eq
o
o
(Eq
appropriatee
appropriat
appropriat
appropriat
th e appropriat e pd f f f f formul a (Eq.. . . . 5.6 ) ) ) int o th e momen t t t equations off f f f ste p (a).. . . .
(a)
(a)
p
(a)
(a)
5.6
5.6))
5.6
5.6
p
ste
ste
th
ste
thee
th
th
e
e
o
s
s
s
s
formul
equation
equation
formul
formul
a
momentt
e
e
e
e
momen
momen
a
momen
equation
o
pd
pd
(Eq
o
pd
th
th
equation
o
th
o
law
law
e
c
e
e
c
laws these are integrall
law
c
integra
integra
th
th
integra
e
ar
e
e
equation
equations for thee
equation
equation
fo
Whil
th
fo
fo
e
e
Lagrangee
Lagrang
e
thes
thes
While in the case of algebraicc law s s s s thes e ar e integra l l l equation s s s s fo r r r r th e Lagrang e
thes
ar
ar
Whil
Whil
Whil
Lagrang
Lagrang
e
e
e
f
n
th
f
cas
f
f
th
th
o
th
o
o
o
e
e
n
e
n
n
e
algebrai
algebrai
algebrai
algebrai
cas
cas
cas
i
e
e
i
e
e
e
e
i
i
multipliers
multipliers
multipliers
m
m
multipliers , , , i i i i in thee cas e e e e o f f f differentia l l l law s the y hav e th e formm off f f f integrodiffer - - -
m
the
o
the
the
o
law
th
o
law
th
o
law
laws theyy
s
o
multipliers,,
o
s
th
th
s
o
integrodiffer
integrodiffer
integrodiffer
integrodiffer--
hav
e
e
hav
th
th
e
e
e
e
th
e
have thee
cas
for
y
for
n
n
for
for
case off
cas
hav
e
n
y
cas
n
differentia
differentia
differentiall
differentia
equations
equations
equations
equations
entia
entia
entiall
entia
entia l l l equations.. . . .
n
Whe
n
,
,
n
,
e
e
n
,
physica
equation
physica
available
equation
Whe
physica
Whe
equation
Whe
differentia
physica
for
equationss
e
available
differentia
differentia
available
for
available
for
m
ar
m
ar
n
ar
l
n
l
ar
l
l
th
an
Whenn physical laws in thee for m o f f f f differentia l l l equation s s s are available, an-- - - -
formm
s
s
s
th
s
th
e
e
e
i
e
i
law
i
law
i
law
law
n
an
an
th
o
an
o
of differentiall
o
o
differentia
differentiall
e
differentia
n
o
differentia
n
a
as shown inn
show
othe r r r approac h (Fig.. . . . 5.1)) ) ) ) i is too discretize th e differentia l l l a s s s s show n i n Chapte r r r
s
s
a
a
show
i
h
i
i
approac
show
h
approac
s
(Fig
t
(Fig
(Fig
n
o
t
t
t
othe
othe
s
otherr
approac
(Fig
othe
approachh
e
5.1
n
discretize
discretize
th
thee
n
th
5.1
Chapte
Chapterr
discretize
discretize
5.1
5.1
Chapte
Chapte
i
i
i
th
n
thuss
thu
thu
n
thu
3.24
obtainin
(difference
a
obtainin
(difference
obtainin
3.24
(difference
(difference
n
obtainingg
33 (Eq . . . 3.24,, , , , p . . . 80) , , , thu s obtainin g ann algebraicc c c c (difference)) ) ) ) equationn o f f f th e
o
(Eq
off
g
g
o
n
3
o
n
3.24
3
3
3.24
e
e
p
th
s
s
th
algebrai
(Eq
equatio
thee
th
equatio
p
equatio
equatio
algebrai
p..
p
(Eq..
n
a
a
80)
a
80)
algebrai
algebrai
(Eq
80),,
80)
n
use--
n
s
s
n
Thi
m
s
n
m
Equatio
s
Equatio
77)
77)
77)
Equatio
Equationn
77)..
Thi
Thi
Thi
h
h
particularl
give
particularl
(p
(p
y
s
y
givenn
y
(p..
use
use
use
approach
approach, whichh
s
(p
particularl
particularl
i
s
for
for
5
whic
n
for m give n i i i inn Equatio n 3. 5 (p . . . 77) . . . Thiss approach , , , , whic h i i i i is particularlyy use - - -
n
for
5
formm
whic
3.
n
3.
approach
approach
give
whic
3.
give
3.55
alread
bee
alread
involvin
alread
bee
involvin
involvingg
bee
beenn
n
n
case
case
case
case
involvin
s
s
s
equations
equations
equations,,
full
fu
fu
i
i
i
partia
partiall
equations
differentia
differentia
differentiall
g
g
differentia
comple
partia
partia
comple
comple
comple
x
ha
has alreadyy
x
ha
ha
x
n
fu l l l i inn casess s s s involvin g complexx partia l l l differentia l l l equations , , , ha s alread y y y bee n
n
n
fu
physica
physica
"Genera
physica
"General knowledgee
3
3
f
f
f
"Genera
"Genera
n
n
n
physica
d
section
d
th
d
n
n
section,,
section
section
th
i
th
e
e
i
n
i
i
i
f
s
knowledg
s
s
discusse
n
discusse
discusse
n
n
Chapterr
discussedd i i inn Chapte r r r 3 i n th e section , , , "Genera l l l l knowledg e i i i i in termss of physicall l l l
Chapte
Chapte
Chapte
e
e
knowledg
knowledg
o
o
term
term
3 in thee
3
o
o
discusse
term
term
n
81..
81
81
p
als
als
beginnin
beginnin
beginning onn
81
se
g
se
se
see alsoo
e
beginnin
e
g
e
g
als
n
n
3.10
3.10
laws,""
laws,
laws, " " " beginnin g o n p.. . . . 76 ; ; ; se e als o Exampl e 3.10 , , , p.. . . . 81 . . .
laws,
p
p
p
p
e
3.10
e
e
laws,
76
o
76
76;;
p
p
o
p
Exampl
Exampl
Exampl
Example 3.10,,
o
76
o
o