Page 141 - Modern Spatiotemporal Geostatistics

122 Modern Spatiotemporal Geostatistics — Chapter 5

data set Xdata lowers the number of possible X(p k) realizations. Equations
5.35 and 5.36 could be viewed as knowledge processing rules. Indeed, just
as certain rules tell us how to measure distances or how to weigh objects,
these equations tell us how to update our evaluation of a situation given new
knowledge.

The Structure of the Modern
Spatiotemporal Geostatistics Paradigm

As mentioned in preceding chapters, classical geostatistics is based on pure
induction (Chapter 1, p. 11) which interprets the relationship between data
and mathematical analysis as a linear one, i.e.,

Data—> Mathematical Fitting — » Prediction an d Testing (5.37)

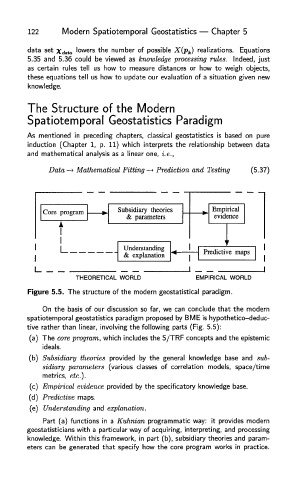
Figure 5.5. The structure of the modern geostatistical paradigm.

On the basis of our discussion so far, we can conclude that the modern
spatiotemporal geostatistics paradigm proposed by BME is hypothetico-deduc-
tive rather than linear, involving the following parts (Fig. 5.5):

(a) Th e core program, which include s the S/TRF concepts and the epistemic
ideals.

(b) Subsidiary theories provide d b y th e genera l knowledg e bas e an d sub-

sidiary parameters (variou s classe s of correlatio n models , space/tim e

metrics, etc.).
(c) Empirical evidence provide d b y the specificator y knowledg e base.

(d) Predictive maps .

(e) Understanding an d explanation.

Part (a) functions in a Kuhnian programmatic way: it provides modern
geostatisticians with a particular way of acquiring, interpreting, and processing
knowledge. Within this framework, in part (b), subsidiary theories and param-
eters can be generated that specify how the core program works in practice.