Page 267 - Modern Spatiotemporal Geostatistics

248 Modern Spatiotemporal Geostatistics — Chapter 12

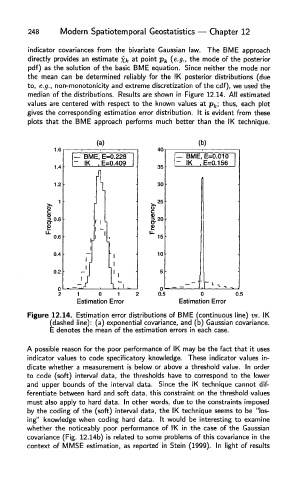
indicator covariances from the bivariate Gaussian law. The BME approach
directly provides an estimate Xk at point p k (e.g., the mode of the posterior
pdf) as the solution of the basic BME equation. Since neither the mode nor
the mean can be determined reliably for the IK posterior distributions (due
to, e.g., non-monotonicity and extreme discretization of the cdf), we used the
median of the distributions. Results are shown in Figure 12.14. All estimated
values are centered with respect to the known values at p k\ thus, each plot
gives the corresponding estimation error distribution. It is evident from these
plots that the BME approach performs much better than the IK technique.

Figure 12.14. Estimation error distributions of BME (continuous line) vs. IK
(dashed line): (a) exponential covariance, and (b) Gaussian covariance.
E denotes the mean of the estimation errors in each case.

A possible reason for the poor performance of IK may be the fact that it uses
indicator values to code specificatory knowledge. These indicator values in-
dicate whether a measurement is below or above a threshold value. In order
to code (soft) interval data, the thresholds have to correspond to the lower
and upper bounds of the interval data. Since the IK technique cannot dif-
ferentiate between hard and soft data, this constraint on the threshold values
must also apply to hard data. In other words, due to the constraints imposed
by the coding of the (soft) interval data, the IK technique seems to be "los-
ing" knowledge when coding hard data. It would be interesting to examine
whether the noticeably poor performance of IK in the case of the Gaussian
covariance (Fig. 12.14b) is related to some problems of this covariance in the
context of MMSE estimation, as reported in Stein (1999). In light of results