Page 147 - Book Hosokawa Nanoparticle Technology Handbook

3.2 SINGLE NANOPARTICLE MOTION IN FLUID FUNDAMENTALS

2
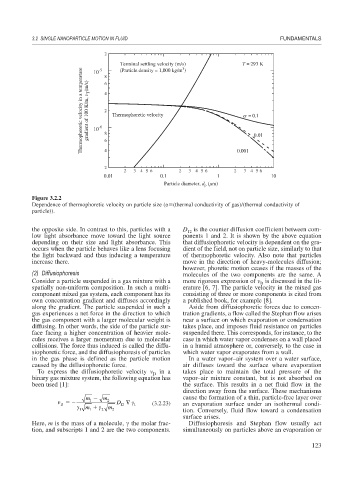
Terminal settling velocity (m/s) T = 293 K
Thermophoretic velocity in a temperature gradient of 100 K/m, v T (m/s) 10 -6 4 2 8 Thermophoretic velocity α = 0.1
3
-5
(Particle density = 1,000 kg/m )
10
8
6

0.01

2 6 4 0.001
2 3 4 5 6 2 3 4 5 6 2 3 4 5 6
0.01 0.1 1 10
Particle diameter, d ( m)
p
Figure 3.2.2
Dependence of thermophoretic velocity on particle size (
(thermal conductivity of gas)/(thermal conductivity of
particle)).

the opposite side. In contrast to this, particles with a D is the counter diffusion coefficient between com-
12
low light absorbance move toward the light source ponents 1 and 2. It is shown by the above equation
depending on their size and light absorbance. This that diffusiophoretic velocity is dependent on the gra-
occurs when the particle behaves like a lens focusing dient of the field, not on particle size, similarly to that
the light backward and thus inducing a temperature of thermophoretic velocity. Also note that particles
increase there. move in the direction of heavy-molecules diffusion;
however, phoretic motion ceases if the masses of the
(2) Diffusiophoresis molecules of the two components are the same. A
Consider a particle suspended in a gas mixture with a more rigorous expression of v is discussed in the lit-
D
spatially non-uniform composition. In such a multi- erature [6, 7]. The particle velocity in the mixed gas
component mixed gas system, each component has its consisting of three or more components is cited from
own concentration gradient and diffuses accordingly a published book, for example [8].
along the gradient. The particle suspended in such a Aside from diffusiophoretic forces due to concen-
gas experiences a net force in the direction to which tration gradients, a flow called the Stephan flow arises
the gas component with a larger molecular weight is near a surface on which evaporation or condensation
diffusing. In other words, the side of the particle sur- takes place, and imposes fluid resistance on particles
face facing a higher concentration of heavier mole- suspended there. This corresponds, for instance, to the
cules receives a larger momentum due to molecular case in which water vapor condenses on a wall placed
collisions. The force thus induced is called the diffu- in a humid atmosphere or, conversely, to the case in
siophoretic force, and the diffusiophoresis of particles which water vapor evaporates from a wall.
in the gas phase is defined as the particle motion In a water vapor–air system over a water surface,
caused by the diffusiophoretic force. air diffuses toward the surface where evaporation
To express the diffusiophoretic velocity v in a takes place to maintain the total pressure of the
D
binary gas mixture system, the following equation has vapor–air mixture constant, but is not absorbed on
been used [1]: the surface. This results in a net fluid flow in the
direction away from the surface. These mechanisms
m m cause the formation of a thin, particle-free layer over
v 1 2 D
(3.2.23)
D 12 1 an evaporation surface under an isothermal condi-

1 m 1
2 m 2 tion. Conversely, fluid flow toward a condensation
surface arises.
Here, m is the mass of a molecule, the molar frac- Diffusiophoresis and Stephan flow usually act
tion, and subscripts 1 and 2 are the two components. simultaneously on particles above an evaporation or

123