Page 61 - Book Hosokawa Nanoparticle Technology Handbook

FUNDAMENTALS CH. 1 BASIC PROPERTIES AND MEASURING METHODS OF NANOPARTICLES
are not observed. As a result, the Si nanowire seems to For example, the dielectric property of the materials
indicate high strength. Furthermore, Young’s modulus is usually measured by the following process. First,
of the nanowire was as small as 1/6 of a micrometer- the capacitance of the sample is estimated by imped-
size specimen. Elastic properties are originated from ance analyzer, followed by the measurement of the
an atomic bonding. The reason why Young’s modulus sample thickness and the surface area of the elec-
of Si nanowire is smaller is probably that the atomic trode. Lastly, the dielectric constant of the sample is
bonding state was changed by decrease in particle size calculated from these data. However, if we use this
below 10nm. method to evaluate the dielectric property, we cannot
Carbon nanotubes have a cylindrical structure of measure the intrinsic dielectric constant of the
graphene sheets, which show excellent mechanical nanoparticles, because the measurement using
properties because of their integrity. Theoretical calcu- the impedance analyzer requires the bottom and the
lation suggests over thousands GPa of elastic modulus top electrodes on the nanoparticles. Deposition of
[5]. In the experimental study, mechanical properties of the electrodes on the nanoparticles seems to be very
CNTs have been evaluated. In bending test, it is difficult.
observed that CNT deformed to undulate [6]. To overcome this problem, some analysis methods
Mechanical properties of a CNT are evaluated using an have been attempted so far by many researchers. For
atomic force microscope. As a result, over 1000 GPa is example, nanoparticles were molded into the pellet
estimated as Young’s modulus [7]. Furthermore, tensile and the capacitance of this pellet was measured by
test in SEM results in 11–63 GPa and 270–950 GPa for impedance analyzer, same as the bulk materials
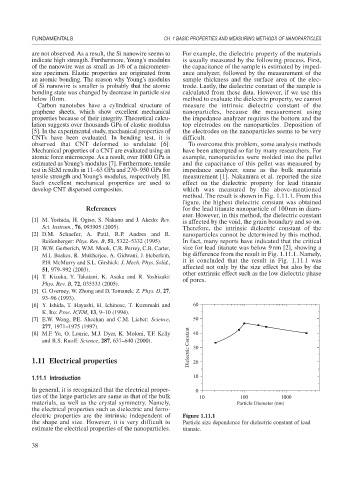
tensile strength and Young’s modulus, respectively [8]. measurement [1]. Nakamura et al. reported the size
Such excellent mechanical properties are used to effect on the dielectric property for lead titanate
develop CNT dispersed composites. which was measured by the above-mentioned
method. The result is shown in Fig. 1.11.1. From this
figure, the highest dielectric constant was obtained
References for the lead titanate nanoparticle of 100nm in diam-
eter. However, in this method, the dielectric constant
[1] M. Yoshida, H. Ogiso, S. Nakano and J. Akedo: Rev. is affected by the void, the grain boundary and so on.
Sci. Instrum., 76, 093905 (2005). Therefore, the intrinsic dielectric constant of the
[2] D.M. Schaefer, A. Patil, R.P. Andres and R. nanoparticles cannot be determined by this method.
Reifenberger: Phys. Rev. B, 51, 5322–5332 (1995). In fact, many reports have indicated that the critical
[3] W.W. Gerberich, W.M. Mook, C.R. Perrey, C.B. Carter, size for lead titanate was below 9nm [2], showing a
M.I. Baskes, R. Mukherjee, A. Gidwani, J. Heberlein, big difference from the result in Fig. 1.11.1. Namely,
it is concluded that the result in Fig. 1.11.1 was
P.H. McMurry and S.L. Girshick: J. Mech. Phys. Solid.,
affected not only by the size effect but also by the
51, 979–992 (2003).
other extrinsic effect such as the low dielectric phase
[4] T. Kizuka, Y. Takatani, K. Asaka and R. Yoshizaki:
of pores.
Phys. Rev. B, 72, 035333 (2005).
[5] G. Overney, W. Zhong and D. Tomanek: Z. Phys. D, 27,
93–96 (1993).
[6] Y. Ishida, T. Hayashi, H. Ichinose, T. Kuzumaki and 60
K. Ito: Proc. ICEM, 13, 9–10 (1994).
[7] E.W. Wong, P.E. Sheehan and C.M. Lieber: Science, 50
277, 1971–1975 (1997).
Dielectric Constant 30
[8] M.F. Yu, O. Lourie, M.J. Dyer, K. Moloni, T.F. Kelly 40
and R.S. Ruoff: Science, 287, 637–640 (2000).

1.11 Electrical properties 20

1.11.1 Introduction 10
In general, it is recognized that the electrical proper- 0
ties of the large particles are same as that of the bulk 10 100 1000
materials, as well as the crystal symmetry. Namely, Particle Diameter (nm)
the electrical properties such as dielectric and ferro-
electric properties are the intrinsic independent of Figure 1.11.1
the shape and size. However, it is very difficult to Particle size dependence for dielectric constant of lead
estimate the electrical properties of the nanoparticles. titanate.

38