Page 220 - Neural Network Modeling and Identification of Dynamical Systems

6.3 SEMIEMPIRICAL MODELING OF AIRCRAFT THREE-AXIS ROTATIONAL MOTION 211

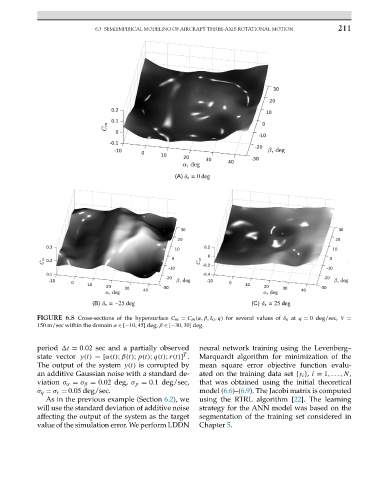
FIGURE 6.8 Cross-sections of the hypersurface C m = C m (α,β,δ e ,q) for several values of δ e at q = 0 deg/sec, V =
150 m/sec within the domain α ∈[−10,45] deg, β ∈[−30,30] deg.

period t = 0.02 secand apartiallyobserved neural network training using the Levenberg–
T
state vector y(t) =[α(t);β(t);p(t);q(t);r(t)] . Marquardt algorithm for minimization of the
The output of the system y(t) is corrupted by mean square error objective function evalu-
an additive Gaussian noise with a standard de- ated on the training data set {y i }, i = 1,...,N,
viation σ α = σ β = 0.02 deg, σ p = 0.1 deg/sec, that was obtained using the initial theoretical
σ q = σ r = 0.05 deg/sec. model (6.6)–(6.9). The Jacobi matrix is computed
As in the previous example (Section 6.2), we using the RTRL algorithm [22]. The learning
will use the standard deviation of additive noise strategy for the ANN model was based on the
affecting the output of the system as the target segmentation of the training set considered in
value of the simulation error. We perform LDDN Chapter 5.