Page 230 - Neural Network Modeling and Identification of Dynamical Systems

6.4 SEMIEMPIRICAL MODELING OF AIRCRAFT LONGITUDINAL TRANSLATIONAL AND ANGULAR MOTION 221
22: break;
23: else
24: r ← r + 1;
25: end if
26: end while
27: if r< R then
¯
28: A ← A;
29: break;
30: else
31: Decrease S max by some amount;
32: end if
33: end while
34: end while

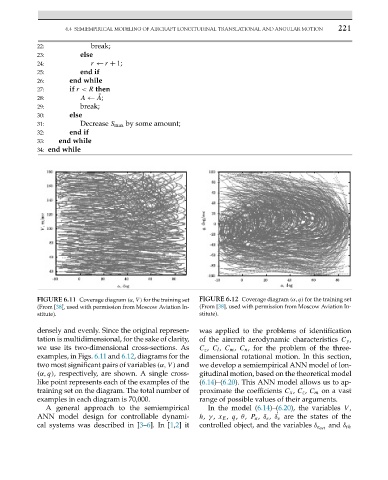
FIGURE 6.11 Coverage diagram (α,V ) for the training set FIGURE 6.12 Coverage diagram (α,q) for the training set
(From [38], used with permission from Moscow Aviation In- (From [38], used with permission from Moscow Aviation In-
stitute). stitute).

densely and evenly. Since the original represen- was applied to the problems of identification
tation is multidimensional, for the sake of clarity, of the aircraft aerodynamic characteristics C y ,
we use its two-dimensional cross-sections. As C z , C l , C m , C n , for the problem of the three-
examples, in Figs. 6.11 and 6.12, diagrams for the dimensional rotational motion. In this section,
two most significant pairs of variables (α,V ) and we develop a semiempirical ANN model of lon-
(α,q), respectively, are shown. A single cross- gitudinal motion, based on the theoretical model
like point represents each of the examples of the (6.14)–(6.20). This ANN model allows us to ap-
training set on the diagram. The total number of proximate the coefficients C x , C z , C m on a vast
examples in each diagram is 70,000. range of possible values of their arguments.
A general approach to the semiempirical In the model (6.14)–(6.20), the variables V ,
ANN model design for controllable dynami- h, γ , x E , q, θ, P a , δ e , ˙ δ e are the states of the
cal systems was described in [3–6]. In [1,2]it controlled object, and the variables δ e act and δ th