Page 228 - Numerical Analysis Using MATLAB and Excel

Symmetry

(
⁄
)
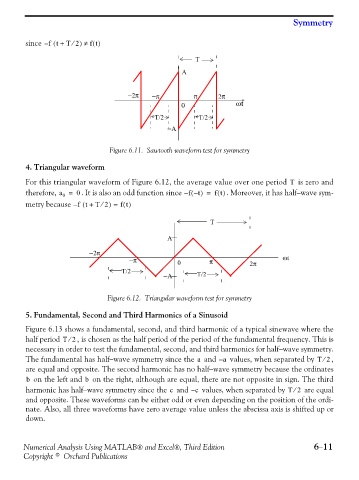
since ft + T 2 ≠ ft()
–
T
A

−2π −π π 2π
0 ωt
T/2 T/2
−A

Figure 6.11. Sawtooth waveform test for symmetry

4. Triangular waveform

For this triangular waveform of Figure 6.12, the average value over one period is zero and
T
therefore, a = 0 . It is also an odd function since f –()– t = ft() . Moreover, it has half−wave sym-
0
⁄
)
metry because ft +( – T 2 = ft()
T

A

−2π
−π 0 π 2π ωt

T/2
−A T/2

Figure 6.12. Triangular waveform test for symmetry

5. Fundamental, Second and Third Harmonics of a Sinusoid
Figure 6.13 shows a fundamental, second, and third harmonic of a typical sinewave where the
⁄
half period T2 , is chosen as the half period of the period of the fundamental frequency. This is
necessary in order to test the fundamental, second, and third harmonics for half−wave symmetry.
a
The fundamental has half−wave symmetry since the and a– values, when separated by T2⁄ ,
are equal and opposite. The second harmonic has no half−wave symmetry because the ordinates
b on the left and on the right, although are equal, there are not opposite in sign. The third
b
harmonic has half−wave symmetry since the and c– values, when separated by T2⁄ are equal
c
and opposite. These waveforms can be either odd or even depending on the position of the ordi-
nate. Also, all three waveforms have zero average value unless the abscissa axis is shifted up or
down.

Numerical Analysis Using MATLAB® and Excel®, Third Edition 6−11
Copyright © Orchard Publications