Page 157 - Numerical Analysis and Modelling in Geomechanics

138 C.L.RAMSHAW AND A.R.SELBY

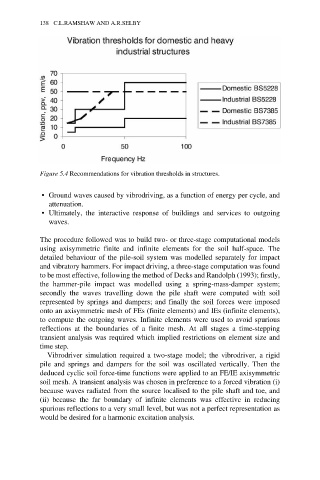
Figure 5.4 Recommendations for vibration thresholds in structures.

• Ground waves caused by vibrodriving, as a function of energy per cycle, and
attenuation.
• Ultimately, the interactive response of buildings and services to outgoing
waves.

The procedure followed was to build two- or three-stage computational models
using axisymmetric finite and infinite elements for the soil half-space. The
detailed behaviour of the pile-soil system was modelled separately for impact
and vibratory hammers. For impact driving, a three-stage computation was found
to be most effective, following the method of Decks and Randolph (1993); firstly,
the hammer-pile impact was modelled using a spring-mass-damper system;
secondly the waves travelling down the pile shaft were computed with soil
represented by springs and dampers; and finally the soil forces were imposed
onto an axisymmetric mesh of FEs (finite elements) and IEs (infinite elements),
to compute the outgoing waves. Infinite elements were used to avoid spurious
reflections at the boundaries of a finite mesh. At all stages a time-stepping
transient analysis was required which implied restrictions on element size and
time step.
Vibrodriver simulation required a two-stage model; the vibrodriver, a rigid
pile and springs and dampers for the soil was oscillated vertically. Then the
deduced cyclic soil force-time functions were applied to an FE/IE axisymmetric
soil mesh. A transient analysis was chosen in preference to a forced vibration (i)
because waves radiated from the source localised to the pile shaft and toe, and
(ii) because the far boundary of infinite elements was effective in reducing
spurious reflections to a very small level, but was not a perfect representation as
would be desired for a harmonic excitation analysis.