Page 202 - Origin and Prediction of Abnormal Formation Pressures

SEISMIC METHODS OF PRESSURE PREDICTION 177

Training Data set; Blue: Actual, Red: Prediction Training Data set (RHOB)
0.5 ...... , ' . . . . * . . . . . . , . . . . . . . ~ ............. 0.5 ....... _~ y~ ....... , ............... , .......... , .......... , ............. , .....
(a)
0.4 0.4 (b) o ~ o ~ = o
0.2 0.2
o o R~= 8'JLe=Ar
o o O==o.~,.j~ -"o o
0
-0.2 -0.2 0 0 ' r - 0
o o
-0.4 -0.4 , Oog
-0.6 -0.6
-0.8 -0.8
0 50 1 O0 150 200 250 300 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6

Testing Data set; Blue: Actual, Grean: Prediction Validation Data set; Blue: Actual, Red: Prediction
0.5 ...................... 9 .............. 9 ...... , ..... 9 ........... 0.5
0.4 0.4
0.3 0.3
0.2 0.2
0,1 0.I
0 0
-0.1 .0.1
.0.2 .0.2
.0.3 ..0.3
-0.4 -0.4
-0.5 ....................................... 0.5
0 20 40 60 80 100 0 20 40 60 80 100
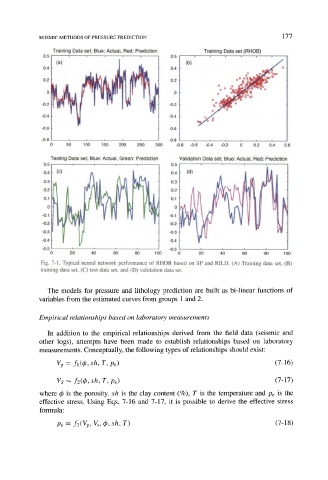
Fig. 7-1. Typical neural network performance of RHOB based on SP and RILD. (A) Training data set, (B)
training data set, (C) test data set, and (D) validation data set.

The models for pressure and lithology prediction are built as bi linear functions of
variables from the estimated curves from groups 1 and 2

Empirical relationships based on laboratory measurements

In addition to the empirical relationships derived from the field data (seismic and
other logs), attempts have been made to establish relationships based on laboratory
measurements. Conceptually, the following types of relationships should exist:
Vp - A@,sh, T, Pe) (7-16)

Vs -- fz(~b, sh, T, Pe) (7-17)
where 4~ is the porosity, sh is the clay content (%), T is the temperature and Pe is the
effective stress. Using Eqs. 7-16 and 7-17, it is possible to derive the effective stress
formula:

Pe -- fz(Vp, Vs, ~b, sh, T) (7-18)