Page 281 - PRINCIPLES OF QUANTUM MECHANICS as Applied to Chemistry and Chemical Physics
P. 281
272 Molecular structure
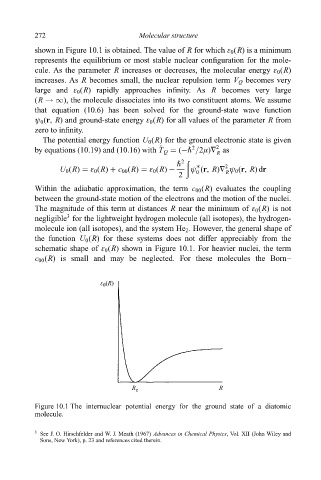
shown in Figure 10.1 is obtained. The value of R for which å 0 (R) is a minimum
represents the equilibrium or most stable nuclear con®guration for the mole-
cule. As the parameter R increases or decreases, the molecular energy å 0 (R)
increases. As R becomes small, the nuclear repulsion term V Q becomes very
large and å 0 (R) rapidly approaches in®nity. As R becomes very large
(R !1), the molecule dissociates into its two constituent atoms. We assume
that equation (10.6) has been solved for the ground-state wave function
ø 0 (r, R) and ground-state energy å 0 (R) for all values of the parameter R from
zero to in®nity.
The potential energy function U 0 (R) for the ground electronic state is given
^
2
2
by equations (10.19) and (10.16) with T Q (ÿ" =2ì)= as
R
" 2
2
U 0 (R) å 0 (R) c 00 (R) å 0 (R) ÿ ø (r, R)= ø 0 (r, R)dr
0
R
2
Within the adiabatic approximation, the term c 00 (R) evaluates the coupling
between the ground-state motion of the electrons and the motion of the nuclei.
The magnitude of this term at distances R near the minimum of å 0 (R) is not
3
negligible for the lightweight hydrogen molecule (all isotopes), the hydrogen-
molecule ion (all isotopes), and the system He 2 . However, the general shape of
the function U 0 (R) for these systems does not differ appreciably from the
schematic shape of å 0 (R) shown in Figure 10.1. For heavier nuclei, the term
c 00 (R) is small and may be neglected. For these molecules the Born±
ε (R)
0
R e R
Figure 10.1 The internuclear potential energy for the ground state of a diatomic
molecule.
3 See J. O. Hirschfelder and W. J. Meath (1967) Advances in Chemical Physics, Vol. XII (John Wiley and
Sons, New York), p. 23 and references cited therein.