Page 25 - Partition & Adsorption of Organic Contaminants in Environmental Systems

16 FUNDAMENTALS OF THE SOLUTION THEORY

If component i is
sparingly soluble
P ° P °
i i

P
i γ >1
i
γ =1
i
γ <1
i

0 ° x 1
i
x i
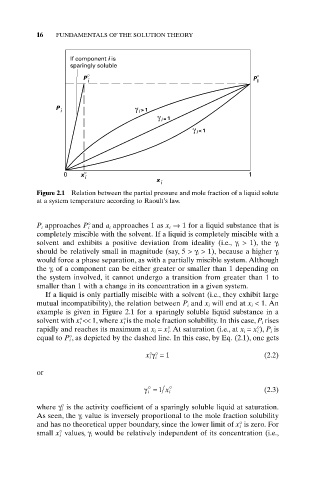
Figure 2.1 Relation between the partial pressure and mole fraction of a liquid solute
at a system temperature according to Raoult’s law.

P i approaches P° i and a i approaches 1 as x i Æ 1 for a liquid substance that is
completely miscible with the solvent. If a liquid is completely miscible with a
solvent and exhibits a positive deviation from ideality (i.e., g i > 1), the g i
should be relatively small in magnitude (say, 5 >g i > 1), because a higher g i
would force a phase separation, as with a partially miscible system. Although
the g i of a component can be either greater or smaller than 1 depending on
the system involved, it cannot undergo a transition from greater than 1 to
smaller than 1 with a change in its concentration in a given system.
If a liquid is only partially miscible with a solvent (i.e., they exhibit large
mutual incompatibility), the relation between P i and x i will end at x i < 1. An
example is given in Figure 2.1 for a sparingly soluble liquid substance in a
solvent with x° i << 1, where x° i is the mole fraction solubility. In this case, P i rises
rapidly and reaches its maximum at x i = x° i . At saturation (i.e., at x i = x° i ), P i is
equal to P° i , as depicted by the dashed line. In this case, by Eq. (2.1), one gets

x° i g° i = 1 (2.2)

or
o o
g i = 1 i x (2.3)

where g° i is the activity coefficient of a sparingly soluble liquid at saturation.
As seen, the g i value is inversely proportional to the mole fraction solubility
and has no theoretical upper boundary, since the lower limit of x° i is zero. For
small x° i values, g i would be relatively independent of its concentration (i.e.,