Page 26 - Partition & Adsorption of Organic Contaminants in Environmental Systems

RAOULT’S LAW 17

P °
i

P
i
s
P i

0 x s ° x 1
i i,id
x i
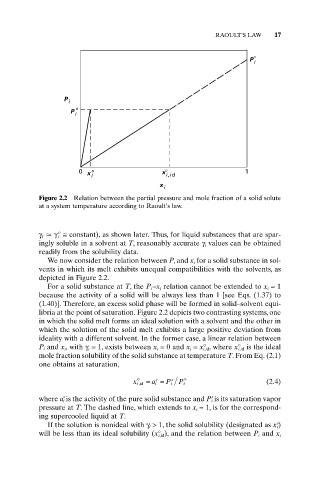
Figure 2.2 Relation between the partial pressure and mole fraction of a solid solute
at a system temperature according to Raoult’s law.

g I g° i @ constant), as shown later. Thus, for liquid substances that are spar-
ingly soluble in a solvent at T, reasonably accurate g i values can be obtained
readily from the solubility data.
We now consider the relation between P i and x i for a solid substance in sol-
vents in which its melt exhibits unequal compatibilities with the solvents, as
depicted in Figure 2.2.
For a solid substance at T, the P i –x i relation cannot be extended to x i = 1
because the activity of a solid will be always less than 1 [see Eqs. (1.37) to
(1.40)]. Therefore, an excess solid phase will be formed in solid–solvent equi-
libria at the point of saturation. Figure 2.2 depicts two contrasting systems, one
in which the solid melt forms an ideal solution with a solvent and the other in
which the solution of the solid melt exhibits a large positive deviation from
ideality with a different solvent. In the former case, a linear relation between
P i and x i, with g i = 1, exists between x i = 0 and x i = x° i,id, where x° i,id is the ideal
mole fraction solubility of the solid substance at temperature T. From Eq. (2.1)
one obtains at saturation,
o
s
x i,id = a i = P i s P i o (2.4)
s
s
where a i is the activity of the pure solid substance and P i is its saturation vapor
pressure at T. The dashed line, which extends to x i = 1, is for the correspond-
ing supercooled liquid at T.
s
If the solution is nonideal with g i > 1, the solid solubility (designated as x i)
will be less than its ideal solubility (x° i,id), and the relation between P i and x i