Page 265 - Phase Space Optics Fundamentals and Applications
P. 265
246 Chapter Eight
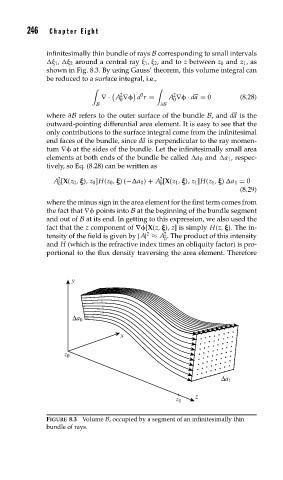
infinitesimally thin bundle of rays B corresponding to small intervals
1 , 2 around a central ray 1 , 2 , and to z between z 0 and z 1 ,as
shown in Fig. 8.3. By using Gauss’ theorem, this volume integral can
be reduced to a surface integral, i.e.,
2 3 2
a
∇· A ∇ d r = A ∇ · d = 0 (8.28)
0
0
B ∂B
where ∂B refers to the outer surface of the bundle B, and d is the
a
outward-pointing differential area element. It is easy to see that the
only contributions to the surface integral come from the infinitesimal
end faces of the bundle, since d is perpendicular to the ray momen-
a
tum ∇ at the sides of the bundle. Let the infinitesimally small area
elements at both ends of the bundle be called a 0 and a 1 , respec-
tively, so Eq. (8.28) can be written as
2
2
A [X(z 0 , ),z 0 ]H(z 0 , )(− a 0 ) + A [X(z 1 , ),z 1 ]H(z 1 , ) a 1 = 0
0 0
(8.29)
where the minus sign in the area element for the first term comes from
the fact that ∇ points into B at the beginning of the bundle segment
and out of B at its end. In getting to this expression, we also used the
fact that the z component of ∇ [X(z, ),z] is simply H(z, ). The in-
2
2
tensity of the field is given by |A| ≈ A . The product of this intensity
0
and H (which is the refractive index times an obliquity factor) is pro-
portional to the flux density traversing the area element. Therefore
y
Δa 0
x
z 0
Δa 1
z 1 z
FIGURE 8.3 Volume B, occupied by a segment of an infinitesimally thin
bundle of rays.