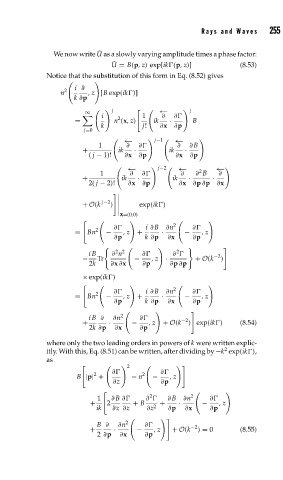Page 274 - Phase Space Optics Fundamentals and Applications

Rays and Waves 255

We now write ˜ U as a slowly varying amplitude times a phase factor:
˜ U = B(p,z) exp[ik (p,z)] (8.53)
Notice that the substitution of this form in Eq. (8.52) gives

i ∂
2
n ,z [B exp(ik )]
k ∂p
j j
∞ ←−
, i 2 1 ∂ ∂
= n (x,z) ik · B
k j! ∂x ∂p
j=0
←− j−1 ←−
1 ∂ ∂ ∂ ∂ B
+ ik · ik ·
( j − 1)! ∂x ∂p ∂x ∂p
j−2
←− ←− 2 ←−
1 ∂ ∂ ∂ ∂ B ∂
+ ik · ik · ·
2( j − 2)! ∂x ∂p ∂x ∂p ∂p ∂x

+ O(k j−2 exp(ik )
)

x=(0,0)

∂ i ∂ B ∂n 2 ∂
2
= Bn − ,z + · − ,z
∂p k ∂p ∂x ∂p
$ %
2
2 2
iB ∂ n ∂ ∂ −2
− Tr − ,z · + O(k )
2k ∂x ∂x ∂p ∂p ∂p
× exp(ik )

∂ i ∂ B ∂n 2 ∂
2
= Bn − ,z + · − ,z
∂p k ∂p ∂x ∂p

iB ∂ ∂n 2 ∂ −2
+ · − ,z + O(k ) exp(ik ) (8.54)
2k ∂p ∂x ∂p
where only the two leading orders in powers of k were written explic-
2
itly. With this, Eq. (8.51) can be written, after dividing by −k exp(ik ),
as
2
∂ ∂
2 2
B |p| + − n − ,z
∂z ∂p

2
1 ∂ B ∂ ∂ ∂ B ∂n 2 ∂
+ 2 + B 2 + · − ,z
ik ∂z ∂z ∂z ∂p ∂x ∂p

B ∂ ∂n 2 ∂ −2
+ · − ,z + O(k ) = 0 (8.55)
2 ∂p ∂x ∂p