Page 370 - Phase Space Optics Fundamentals and Applications

Phase Space in Ultrafast Optics 351

u δu
Height y Height y Height δy u

Optical axis Optical axis Optical axis
(a) (c) (e)
δy
Angle y nu Angle y nδu Angle nu

Height Height Height
(b) (d) (f )

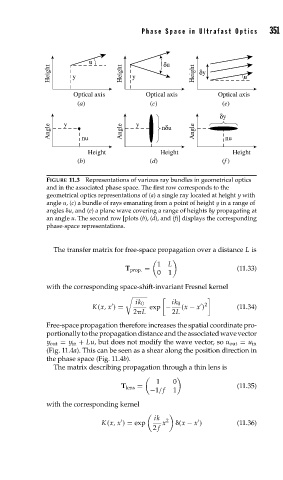
FIGURE 11.3 Representations of various ray bundles in geometrical optics
and in the associated phase space. The first row corresponds to the
geometrical optics representations of (a) a single ray located at height y with
angle u,(c) a bundle of rays emanating from a point of height y in a range of
angles u, and (e) a plane wave covering a range of heights y propagating at
an angle u. The second row [plots (b), (d), and (f)] displays the corresponding
phase-space representations.

The transfer matrix for free-space propagation over a distance L is

1 L
T prop. = (11.33)
0 1
with the corresponding space-shift-invariant Fresnel kernel

ik 0 ik 0
2
K(x, x ) = exp − (x − x ) (11.34)
2 L 2L
Free-space propagation therefore increases the spatial coordinate pro-
portionallytothepropagationdistanceandtheassociatedwavevector
y out = y in + Lu, but does not modify the wave vector, so u out = u in
(Fig. 11.4a). This can be seen as a shear along the position direction in
the phase space (Fig. 11.4b).
The matrix describing propagation through a thin lens is

1 0
T lens = (11.35)
−1/f 1
with the corresponding kernel

ik

K(x, x ) = exp x 2 (x − x ) (11.36)
2 f