Page 371 - Phase Space Optics Fundamentals and Applications
P. 371
352 Chapter Eleven
Height Height
L
(a) (c)
Angle Angle
Height Height
(b) (d)
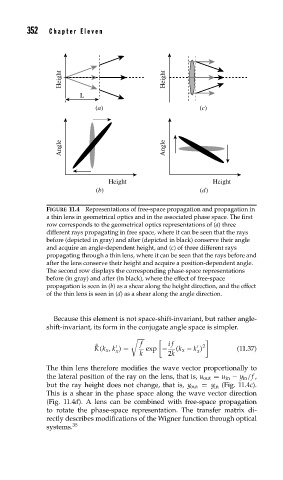
FIGURE 11.4 Representations of free-space propagation and propagation in
a thin lens in geometrical optics and in the associated phase space. The first
row corresponds to the geometrical optics representations of (a) three
different rays propagating in free space, where it can be seen that the rays
before (depicted in gray) and after (depicted in black) conserve their angle
and acquire an angle-dependent height, and (c) of three different rays
propagating through a thin lens, where it can be seen that the rays before and
after the lens conserve their height and acquire a position-dependent angle.
The second row displays the corresponding phase-space representations
before (in gray) and after (in black), where the effect of free-space
propagation is seen in (b) as a shear along the height direction, and the effect
of the thin lens is seen in (d) as a shear along the angle direction.
Because this element is not space-shift-invariant, but rather angle-
shift-invariant, its form in the conjugate angle space is simpler.
f if
2
˜ ˜ K(k x ,k ) = exp − (k x − k ) (11.37)
x x
k 2k
The thin lens therefore modifies the wave vector proportionally to
the lateral position of the ray on the lens, that is, u out = u in − y in /f ,
but the ray height does not change, that is, y out = y in (Fig. 11.4c).
This is a shear in the phase space along the wave vector direction
(Fig. 11.4d). A lens can be combined with free-space propagation
to rotate the phase-space representation. The transfer matrix di-
rectly describes modifications of the Wigner function through optical
systems. 35