Page 249 - Photodetection and Measurement - Maximizing Performance in Optical Systems

Multiple Channel Detection

242 Chapter Eleven

WAL(n,N) R L
PD
LED1 + A Demod.
λ 1 outputs
-
WAL(m,N)
λ 2 Ch. 1
LED2 X ± 1
WAL(n,N)
Measurement Ch. 2
system X ± 1

WAL(m,N)
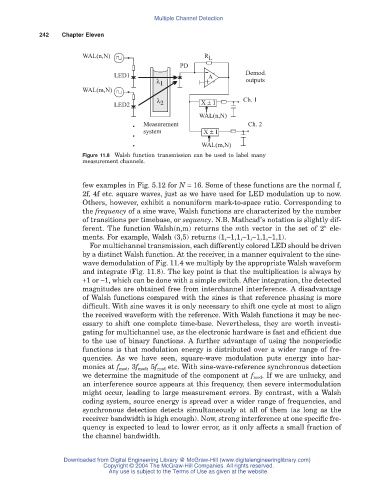
Figure 11.8 Walsh function transmission can be used to label many
measurement channels.

few examples in Fig. 5.12 for N = 16. Some of these functions are the normal f,
2f, 4f etc. square waves, just as we have used for LED modulation up to now.
Others, however, exhibit a nonuniform mark-to-space ratio. Corresponding to
the frequency of a sine wave, Walsh functions are characterized by the number
of transitions per timebase, or sequency. N.B. Mathcad’s notation is slightly dif-
n
ferent. The function Walsh(n,m) returns the mth vector in the set of 2 ele-
ments. For example, Walsh (3,5) returns (1,-1,1,-1,-1,1,-1,1).
For multichannel transmission, each differently colored LED should be driven
by a distinct Walsh function. At the receiver, in a manner equivalent to the sine-
wave demodulation of Fig. 11.4 we multiply by the appropriate Walsh waveform
and integrate (Fig. 11.8). The key point is that the multiplication is always by
+1 or -1, which can be done with a simple switch. After integration, the detected
magnitudes are obtained free from interchannel interference. A disadvantage
of Walsh functions compared with the sines is that reference phasing is more
difficult. With sine waves it is only necessary to shift one cycle at most to align
the received waveform with the reference. With Walsh functions it may be nec-
essary to shift one complete time-base. Nevertheless, they are worth investi-
gating for multichannel use, as the electronic hardware is fast and efficient due
to the use of binary functions. A further advantage of using the nonperiodic
functions is that modulation energy is distributed over a wider range of fre-
quencies. As we have seen, square-wave modulation puts energy into har-
monics at f mod, 3f mod, 5f mod etc. With sine-wave-reference synchronous detection
we determine the magnitude of the component at f mod. If we are unlucky, and
an interference source appears at this frequency, then severe intermodulation
might occur, leading to large measurement errors. By contrast, with a Walsh
coding system, source energy is spread over a wider range of frequencies, and
synchronous detection detects simultaneously at all of them (as long as the
receiver bandwidth is high enough). Now, strong interference at one specific fre-
quency is expected to lead to lower error, as it only affects a small fraction of
the channel bandwidth.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.