Page 114 - Photonics Essentials an introduction with experiments

Light-Emitting Diodes

108 Photonic Devices

3
space = 2 · – k . The number of k-states between k and k + dk is the
4
3
2
surface area = (d/dk)E(k) = 8 k dk. So the density of states in k-space
2
is dN = 8 k dk. Starting with Eq. 6.4, we can derive the energy densi-
ty of states:
2m
k = [E(k) – E g ]
2
2
1/2
2m
k = [E – E g ]

1/2 –1/2
m
dk = [E(k) – E g ] dE (6.5)
2
2
So the density of states can be written as
1/2 1/2
2m
m
2
dN = 8 k dk = 8 (E – E g )· (E – E g ) dE
2

2
2
dN 8 m 3/2 2
= (E – E g ) 1/2 (6.6)
dE 3
1/2
Thus, the density of states is proportional to (E – E g ) .

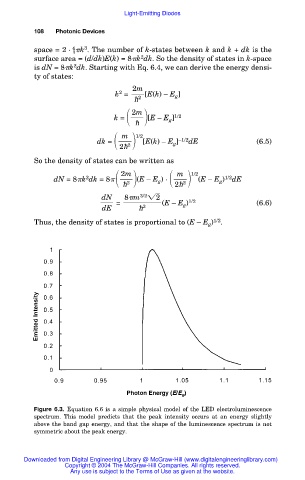
Photon Energy (E/E g )

Figure 6.3. Equation 6.6 is a simple physical model of the LED electroluminescence
spectrum. This model predicts that the peak intensity occurs at an energy slightly
above the band gap energy, and that the shape of the luminescence spectrum is not
symmetric about the peak energy.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.