Page 115 - Photonics Essentials an introduction with experiments

Light-Emitting Diodes

Light-Emitting Diodes 109

The probability that a state is occupied is given by Boltzmann sta-
tistics, that is,

Pr = const · e –(E–E g )/kT
The probability that an optical transition takes place is the square
of the optical matrix element M. It is a constant with a weak depend-
ence on energy, and its value is written as M . We can assemble all
2
these elements to derive an expression for the energy spectrum of the
emitted radiation I(E):
I(E) = K 0 ·(E – E g ) 1/2 · e –(E–E g )/kT (6.7)

where K 0 is a constant, and E is the energy of the emitted photon.
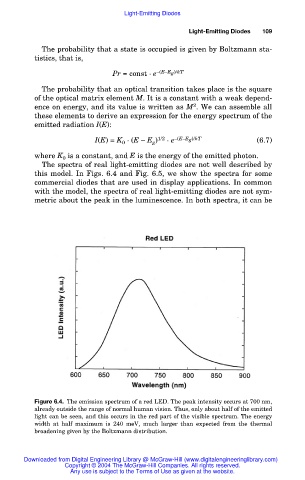
The spectra of real light-emitting diodes are not well described by
this model. In Figs. 6.4 and Fig. 6.5, we show the spectra for some
commercial diodes that are used in display applications. In common
with the model, the spectra of real light-emitting diodes are not sym-
metric about the peak in the luminescence. In both spectra, it can be

Figure 6.4. The emission spectrum of a red LED. The peak intensity occurs at 700 nm,
already outside the range of normal human vision. Thus, only about half of the emitted
light can be seen, and this occurs in the red part of the visible spectrum. The energy
width at half maximum is 240 meV, much larger than expected from the thermal
broadening given by the Boltzmann distribution.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.