Page 305 - Physical Principles of Sedimentary Basin Analysis

9.1 Equation for flexure of a plate 287

z

z(x)
φ R

α 2
α 1 x
dx
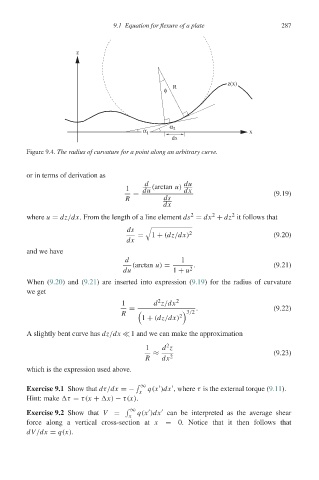
Figure 9.4. The radius of curvature for a point along an arbitrary curve.

or in terms of derivation as
d du
1 du (arctan u) dx
= (9.19)
R ds
dx
2
2
2
where u = dz/dx. From the length of a line element ds = dx + dz it follows that
ds !
= 1 + (dz/dx) 2 (9.20)
dx
and we have
d 1
(arctan u) = . (9.21)
du 1 + u 2
When (9.20) and (9.21) are inserted into expression (9.19) for the radius of curvature
we get
2
1 d z/dx 2
. (9.22)
R =
2 3/2
1 + (dz/dx)
A slightly bent curve has dz/dx
1 and we can make the approximation

2
1 d z
≈ (9.23)
R dx 2
which is the expression used above.
∞

Exercise 9.1 Show that dτ/dx =− q(x )dx , where τ is the external torque (9.11).
x
Hint: make τ = τ(x + x) − τ(x).
∞

Exercise 9.2 Show that V = q(x )dx can be interpreted as the average shear
x
force along a vertical cross-section at x = 0. Notice that it then follows that
dV/dx = q(x).